The following is a brief overview of some common concepts regarding vector-based math for lines and planes in 3-D space:
Direction Angles/Cosines
Unit Vector
Dot Product
Vector Projection
Scalar Projection
Cross Product
Scalar Triple Product
Vector Equation of a Line
Parametric Equations of a Line
Symmetric Equations of a Line
Vector Equation of a Plane
Scalar Equation of a Plane
Distance from a Point in Space to a Line
Distance from a Point in Space to a Plane
Distance Between Two Parallel Planes
Direction Angles and Direction Cosines:
Directions angles are the angles made between a vector and the positive x,y and z axes. Direction cosines are the cosines of those angles. Given the vector "a" (shown below):
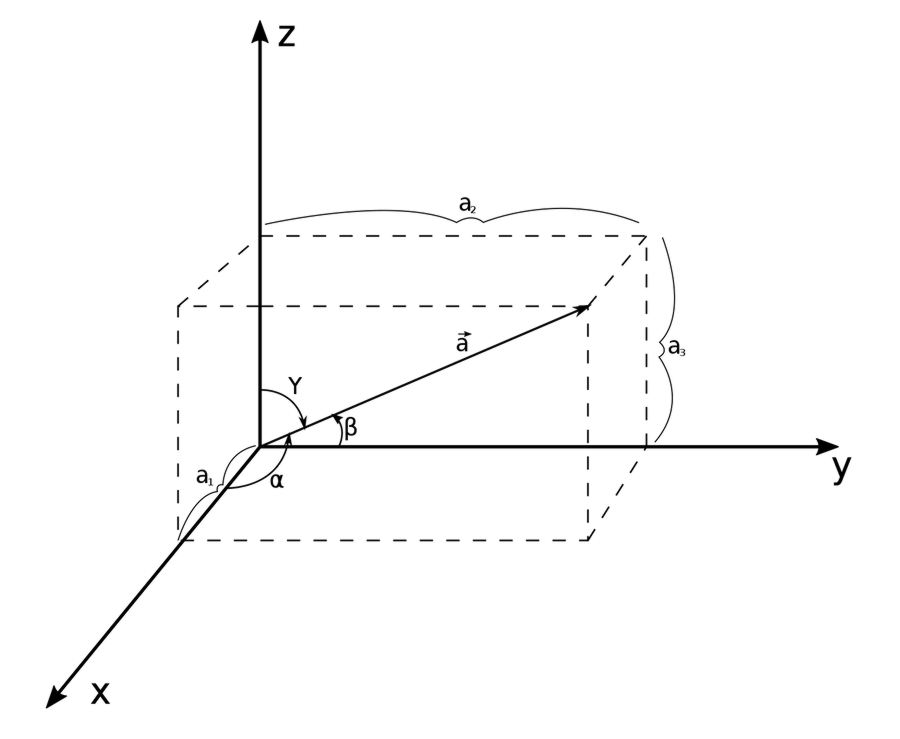
...where: $$ \vec{a} = \langle a_1, a_2, a_3 \rangle = \langle |a|\cos \alpha , |a|\cos \beta, |a| \cos \Upsilon \rangle$$ ...the direction cosines and direction angles can be found through the following:
Direction Cosines:
$$ \cos\alpha = \frac{a_1}{|a|} ,\; \cos \beta = \frac{a_2}{|a|}, \; \cos \Upsilon = \frac{a_3}{|a|} $$
Direction Angles:
$$ \alpha = cos^{-1} \Big( \frac{a_1}{|a|} \Big), \; \beta = cos^{-1} \Big( \frac{a_2}{|a|} \Big) , \; \Upsilon = cos^{-1} \Big( \frac{a_3}{|a|} \Big)$$
Unit vector:
Given a vector "a", the unit vector of "a" has a length (magnitude) of 1 in the same direction of "a". $$ \hat{a} = unit \; vector \; in \; direction \; of \; \vec{a} $$ $$ \;\; = \frac{\vec{a}}{|\vec{a}|} \;\;\;\;\;, where \; |\vec{a}| = magnitude \; of \; \vec{a} $$ $$ \hat{a} = \frac{\vec{a}}{\sqrt{(a_1)^2+(a_2)^2+(a_3)^2}} $$
Dot Product:
Given vectors "a" and "b", where: $$ \vec{a} = \langle a_1, a_2, a_3 \rangle $$ $$ \vec{b} = \langle b_1, b_2, b_3 \rangle $$
...the dot product of "a" and "b" is: $$ \vec{a} \cdot \vec{b} = a_1b_1 + a_2b_2 + a_3b_3 $$ or: $$ \vec{a} \cdot \vec{b} = |\vec{a}| |\vec{b}| \cos \theta $$ ...where: $$ |\vec{a}| \;and\; |\vec{b}| = magnitudes \; of \vec{a} \;and\; \vec{b}$$ ...and: $$ \theta = angle \; between \; \vec{a} \;and\; \vec{b} \; when \; placed \; tail \; to \; tail. $$ note: The result of the dot product is a scalar (not a vector).
Also note that if: $$ \vec{a} \cdot \vec{b} = 0 $$ then the vectors are orthogonal (90 degrees apart).
Vector Projection:
The vector projection of vector "b" onto a vector "a" is known as a "vector projection" and is symbolized as: $$ proj_{\vec{a}}\vec{b} $$ Graphically it looks like the following:
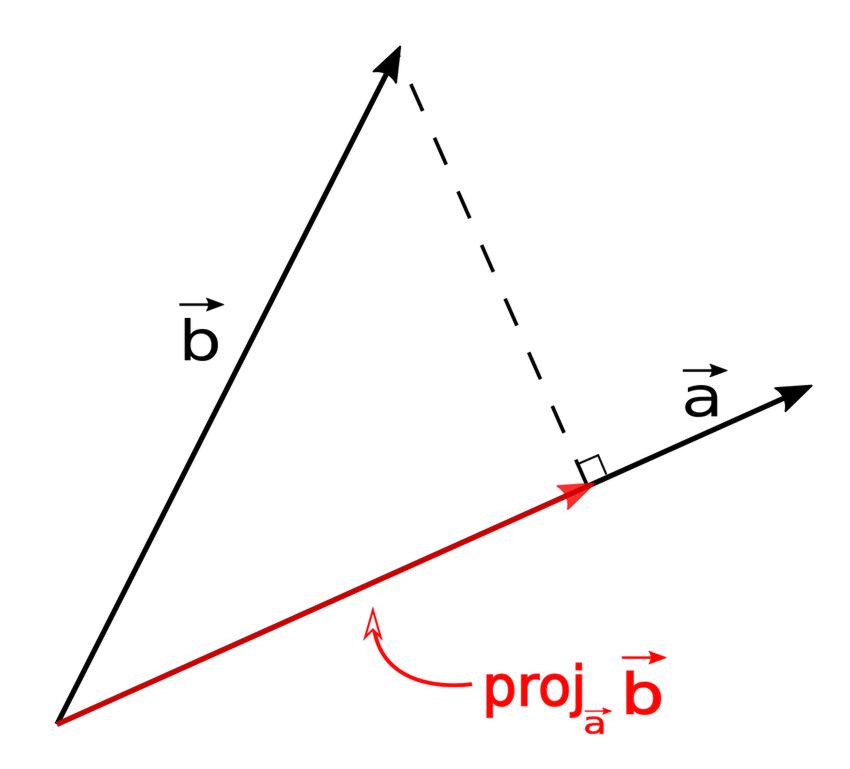
One way of thinking about vector projection is to imagine rays of light shining towards vector "a" at perpendicular angles all along its length. The shadow cast along "a" as a result of the rays of light hiting "b" is the vector projection of "b" onto "a". Mathematically we have the following expression for this vector projection: $$ proj_{\vec{a}}\vec{b} = \Big( \frac{\vec{a} \cdot \vec{b}}{|\vec{a}|^2} \Big) \vec{a} $$ ...where: $$ \qquad |\vec{a}|^2 = \vec{a} \cdot \vec{a} $$ Note that the result of a vector projection is a vector quantity.
Scalar Projection:
The "scalar projection of vector "b" onto vector "a" (sometimes called "component projection") is the signed magnitude of the vector projection. In other words it is the length of the resulting vector projection. It is symbolized as: $$ comp_{\vec{a}}\vec{b} $$ (shown below)
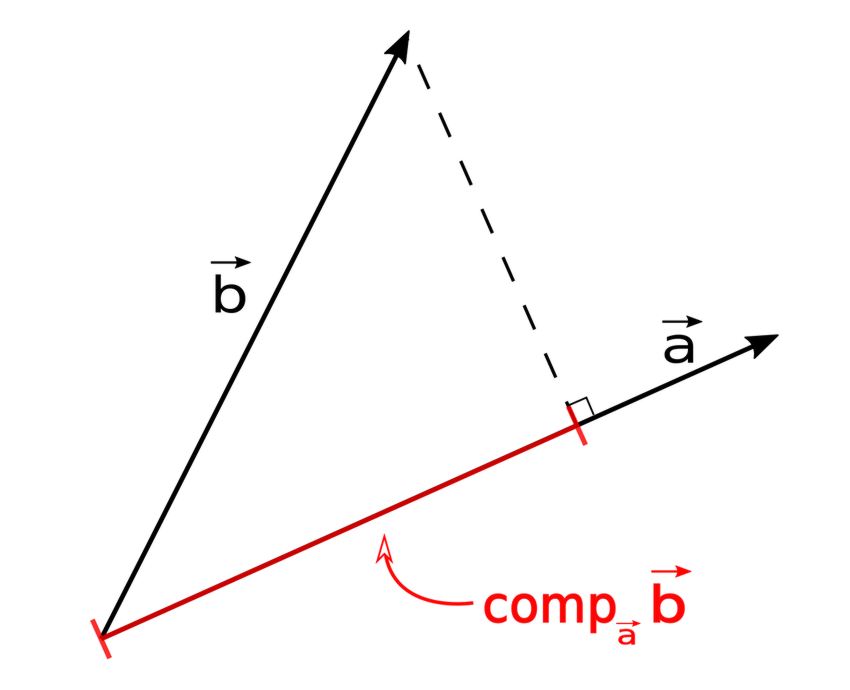
Mathematically, this scalar projection is defined as: $$ comp_{\vec{a}}\vec{b} = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}|} $$ Note that the result of a scalar projection is a scalar quantity.
Cross Product:
The cross product of two vectors produces a vector that is perpendicular to both.. Given the following two vectors:
$$ \vec{a} = \langle a_1, a_2, a_3 \rangle $$
$$ \vec{b} = \langle b_1, b_2, b_3 \rangle $$
The cross product of those two vectors can be found by evaluating the following determinant:
$$
\vec{a} \times \vec{b} =
\begin{vmatrix}
\hat{i}&\hat{j}&\hat{k}\\
a_1&a_2&a_3\\
b_1&b_2&b_3\\
\end{vmatrix}
$$
$$
\qquad \;= \begin{vmatrix}
a_2&a_3\\
b_2&b_3\\
\end{vmatrix}
\hat{i}
\;\; -
\begin{vmatrix}
a_1&a_3\\
b_1&b_3\\
\end{vmatrix}
\hat{j}
\;\; +
\begin{vmatrix}
a_1&a_2\\
b_1&b_2\\
\end{vmatrix}
\hat{k}
$$
$$
\qquad \; = (a_2b_3-a_3b_2)\hat{i} - (a_1b_3-a_3b_1)\hat{j} + (a_1b_2-a_2b_1)\hat{k}
$$
Also, if:
$$ \vec{a} \times \vec{b} = 0 $$
...then the two vectors are parallel.
Additionally, the length of this resulting cross product vector can be defined as:
$$ |\vec{a} \times \vec{b}| = |\vec{a}| |\vec{b}| \sin \theta$$
Lastly, a vector crossed by itself results in zero:
$$ \vec{a} \times \vec{a} = 0 $$
Scalar Triple Product:
The scalar triple product can be used to find the volume of a parallelepiped. When given three vectors, it is found by evaluating the following determinant: $$ \vec{a} \cdot (\vec{b} \times \vec{c}) = \begin{vmatrix} a_1&a_2&a_3\\ b_1&b_2&b_3\\ c_1&c_2&c_3\\ \end{vmatrix} $$ Additionally, note that: $$ \vec{a} \cdot (\vec{b} \times \vec{c}) = \vec{c} \cdot (\vec{a} \times \vec{b}) $$
Vector Equation of a Line:
Consider the following 3-D graph of a line "L":
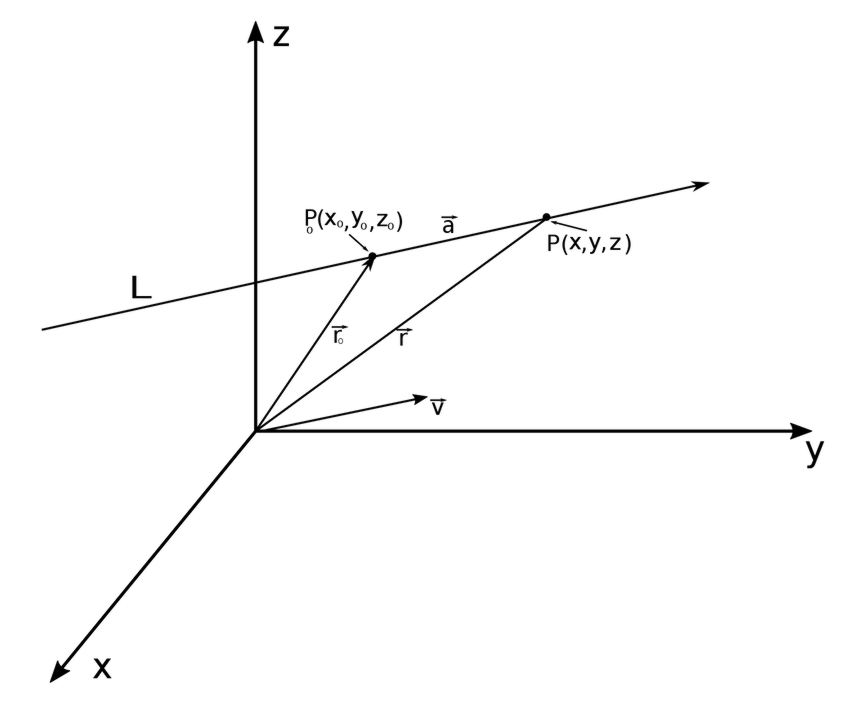
Let P_0 and P be points on line "L" and let "r" and "r_0" be position vectors to each of those points. The vector "a" represents the vector from point P_0 to point P. Additionally, "v" is a vector that is parallel to line "L". By the triangle law for vector addition we have: $$ \vec{r} = \vec{r}_0 + \vec{a} $$ However, since vectors "a" and "v" are parallel, there must exist some scalar value (t) such that: $$ \vec{a} = t\vec{v} $$ Therefore we have the following vector equation for a line:
$$ \vec{r} = \vec{r}_0 + t\vec{v} = vector \; equation \; for \; line \; "L"$$
For every value of "t", we get a position vector "r" for a point on line "L". As the value of "t" is varied, the line "L" is traced out by the tip of vector "r".
Parametric Equations of a Line:
Given a line that passes through a point: $$ P_0(x_0,y_0,z_0) $$ and is parallel to the vector: $$ \vec{v} = \langle a,b,c \rangle $$ ...where a,b and c are the "direction numbers" of the line, the parametric equations for the line is: $$ x = x_0+at $$ $$ y = y_0+bt $$ $$ z = z_0+ct $$ Each value of t gives a single point on the line.
Symmetric Equations of a Line:
If we take the parametric equations for a line and solve for "t" we get: $$ x = x_0+at \qquad, y = y_0+bt \qquad, z = z_0+ct $$ $$ t = \frac{x-x_0}{a} \qquad , t = \frac{y-y_0}{b} \qquad, t = \frac{z-z_0}{c} $$ This gives us the following expression for t: $$ t = \frac{x-x_0}{a} = \frac{y-y_0}{b} = \frac{z-z_0}{c} $$ ...where a,b and c are the "direction numbers" of the line.
Vector Equation of a Plane:
Consider the following graph of a plane:
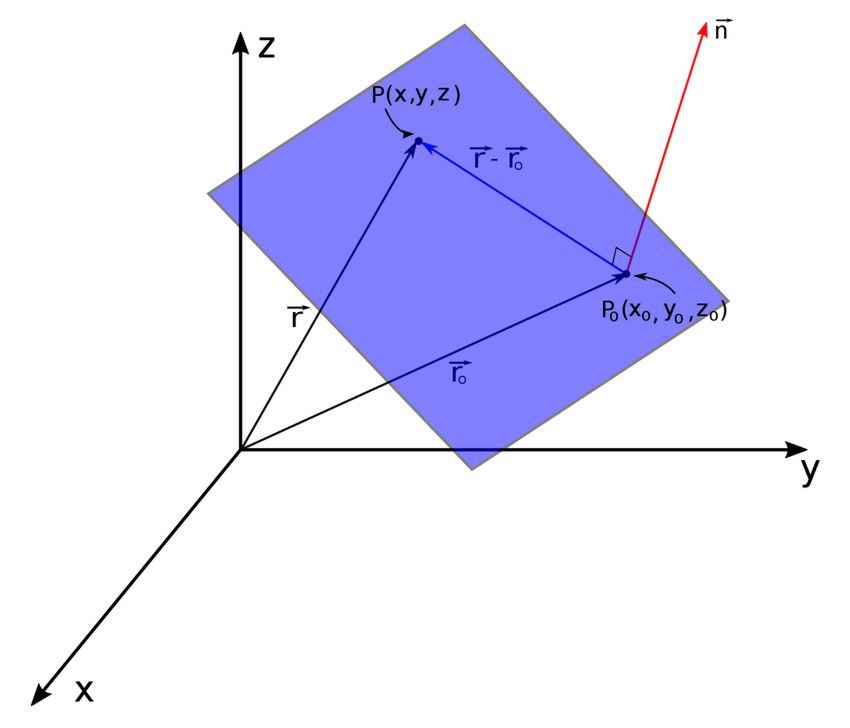
...where: $$ P,P_0 = points \; in \; plane $$ $$ \vec{r}, \vec{r}_0 = position \; vectors \; of \; pts. \; P,P_0 $$ $$ \vec{r} - \vec{r}_0 = \langle P(x,y,z)-P_0(x_0,y_0,z_0) \rangle $$ $$ \vec{n} = \langle a,b,c \rangle = vector \; orthogonal \; to \; plane $$ $$ \vec{r} = \langle x,y,z \rangle $ = vector \; to \; point \; on \; plane$$ $$ \vec{r}_0 = \langle x_0, y_0, z_0 \rangle = vector \; to \; point \; on \; plane $$ The vector equation of a plane is: $$ \vec{n} \cdot (\vec{r}-\vec{r}_0) = 0 $$ ...which can also be written as: $$ \vec{n} \cdot \vec{r} = \vec{n} \cdot \vec{r}_0 $$
Scalar Equation of a Plane:
The scalar equation for a plane is: $$ a(x-x_0)+b(y-y_0)+c(x-x_0)=0 $$ If we collect like terms in the above equation we get the linear equation of the plane: $$ ax+by+cz+d=0 $$
Distance from a Point in Space to a Line:
Consider the following graph showing a point in space and a line:
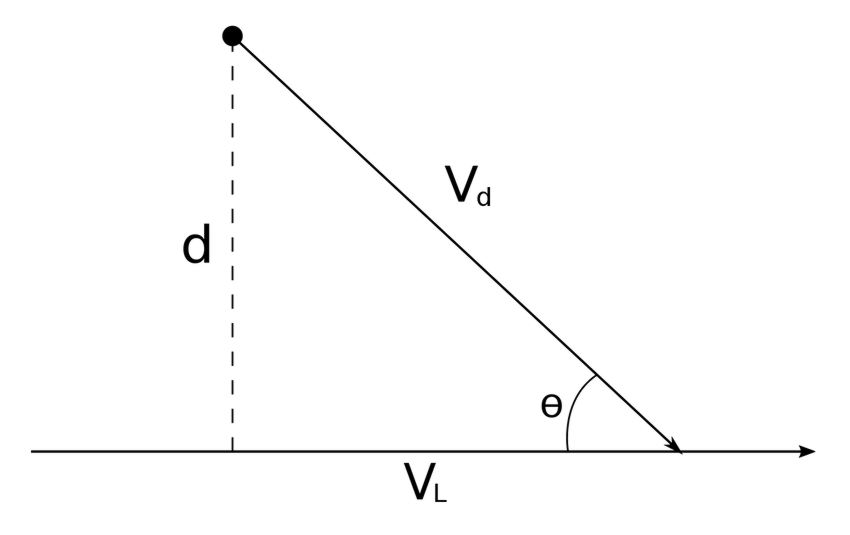
In order to determine the distance (d) from the point to the line: $$1) \; Get \; the \; direction \; vector \; of \; the \; line \; (\vec{V}_L) $$ $$2) \; Find \; a \; coordinate \; of \; a \; point \; on \; the \; line $$ $$ \quad (Set \; "t" \; equal \; to \; number \; in \; parametric \; eqns.)$$ $$ 3) \; Get \; the \; direction \; vector \; from \; pt. \; in \; space \; to \; pt. \; on \; line. (\vec{V}_d)$$ The distance is found through the following: $$ d = \frac{|\vec{V}_d \times \vec{V}_L|}{|\vec{V}_L|} $$ Recall that: $$ \qquad \quad|\vec{V}_d \times \vec{V}_L| = |\vec{V}_d | |\vec{V}_L| \sin(\theta) $$ $$ Therefore: $$
$$ d = |\vec{V}_d| \sin(\theta) $$
Distance from a Point in Space to a Plane:
1) Determine a point on the plane by setting y and z of the plane equation to zero and getting a point such as the following: $$ (number,0,0) $$ 2) Determine the vector from this point on the plane (P0) to the point in space (P1). $$ This \; vector\; = \vec{b} $$ 3) Get the normal vector of the plane: $$ \qquad \vec{n} = \langle a,b,c \rangle $$ The distance from the pt. in space to the plane is now found by: $$ d = comp_{\vec{n}}\vec{b} = \frac{\vec{n} \cdot \vec{b}}{|\vec{n}|} $$
Distance Between Two Parallel Planes:
$$ D = \frac{ax_1+by_1+cz_1+d}{\sqrt{a^2+b^2+c^2}} $$ ...where: $$ (x_1, y_1, z_1) \; is \; pt. \; on \; plane $$ $$ a,b,c = coefficients \; of \; the \; plane \; that \; doesn't \; contain \; the \; above \; pt. $$
