Given the following two signals:
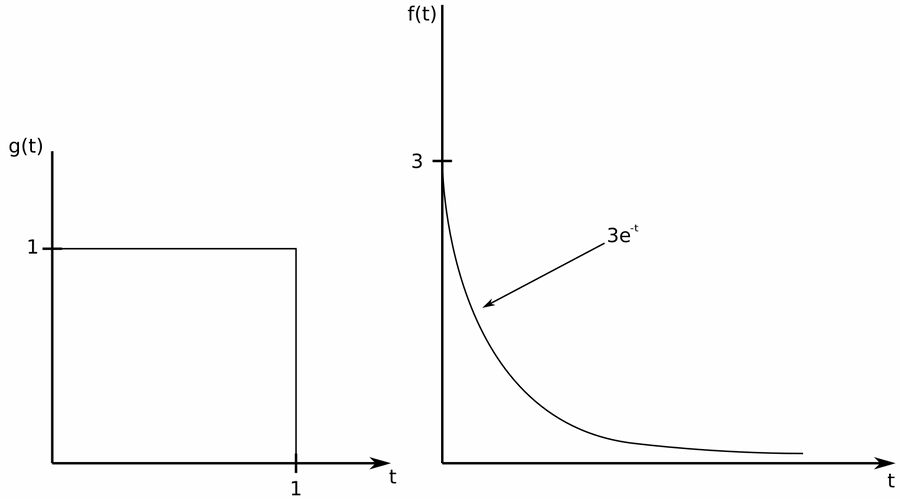
Use the graphical method to determine the convolution: $$ h(t) = g(t) * f(t) $$
Once again, we proceed by following the steps used to evaluate the convolution graphically (outlined in the convolution introduction page).
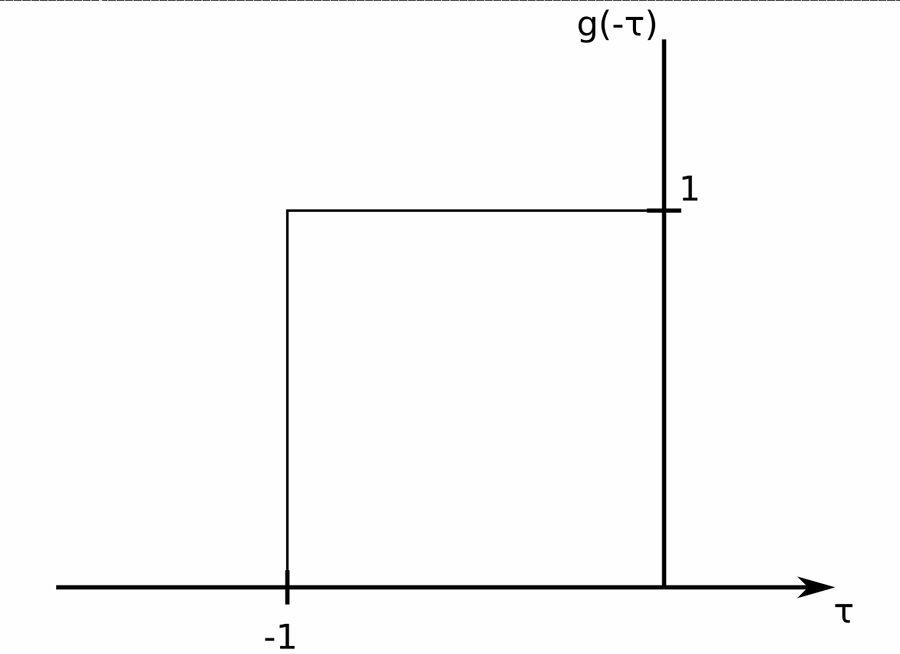
1) Folding: Reflect g(t) about the vertical axis
This gives us $$g(-\tau):$$
2) Shift:
$$ We \; now \; shift \; g(-\tau) \; by \; "t" $$
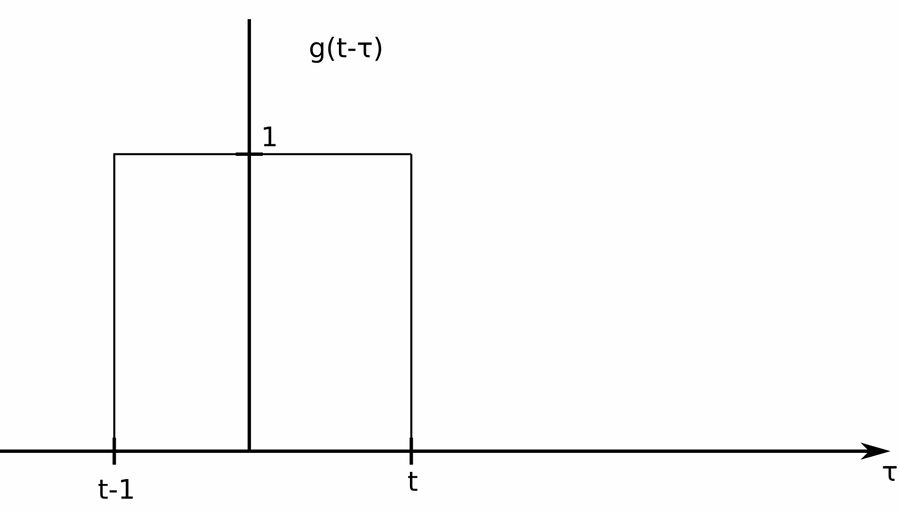
3 and 4) For different values of "t", multiply the functions and calculate the area under the product
$$ For \; t \lt 0, \; the \; signals \; don't \; overlap $$ $$ \qquad h(t) = 0, \; t \lt 0 $$ $$ $$ $$ For \; 0 \lt t \lt 1 \; we \; have: $$
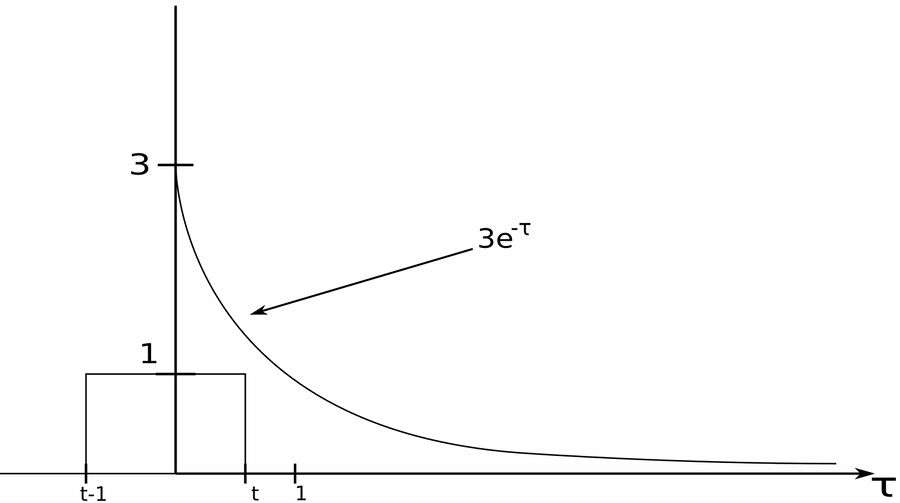
We can see that the two signals overlap between 0 and t. $$ \begin{align} h(t) &= \int_{0}^{t} g(t-\tau)f(\tau) \; d\tau \\\\ &= 3 \int_{0}^{t} e^{-\tau} \; d\tau \\\\ &= 3\Big[ \frac{1}{-1}e^{-\tau} \Big] \Big|^t_{0} \\\\ &= -3[e^{-\tau} \Big|^t_{0} \\\\ &= -3[e^{-t}-1] \end{align} $$
$$ h(t) = 3-3e^{-t} \;,\;\;0 \lt t \lt 1 $$
$$ For \; t \gt 1 \; we \; have: $$
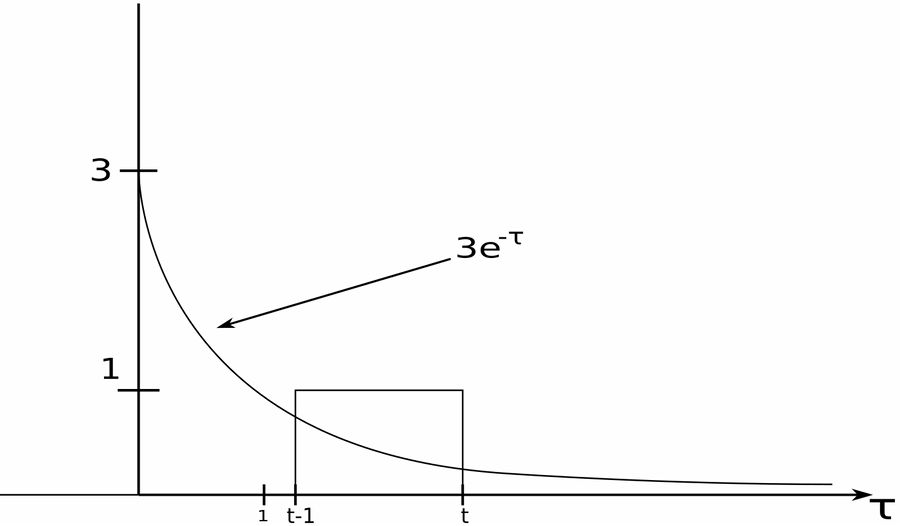
We can see that the two signals overlap between t-1 and t. $$ \begin{align} h(t) &= \int_{t-1}^{t} g(t-\tau)f(\tau) \; d\tau \\\\ &= 3 \int_{t-1}^{t} e^{-\tau} d\tau \\\\ &= -3[e^{-\tau}] \Big|^t_{t-1} \\\\ &= -3 [e^{-t} - e^{-(t-1)}] \end{align} $$
$$ h(t) = -3e^{-t} + 3e^{1-t} \;,\;\; t \gt 1 $$
Our final answer for the convolution is
$$ h(t) = \left\{ \begin{array}{ll} 3-3e^{-t} \;\;,\;\; & 0 \lt t \lt 1 \\ 3e^{1-t} - 3e{-t} \;\;,\;\; & t \gt 1 \end{array} \right. $$
In the next example, we will see how the convolution integral can be used to determine the output voltage of a circuit.
Continue on to example problem #3 (involving the convolutio integral and circuit analysis)...
