Given the following circuit:
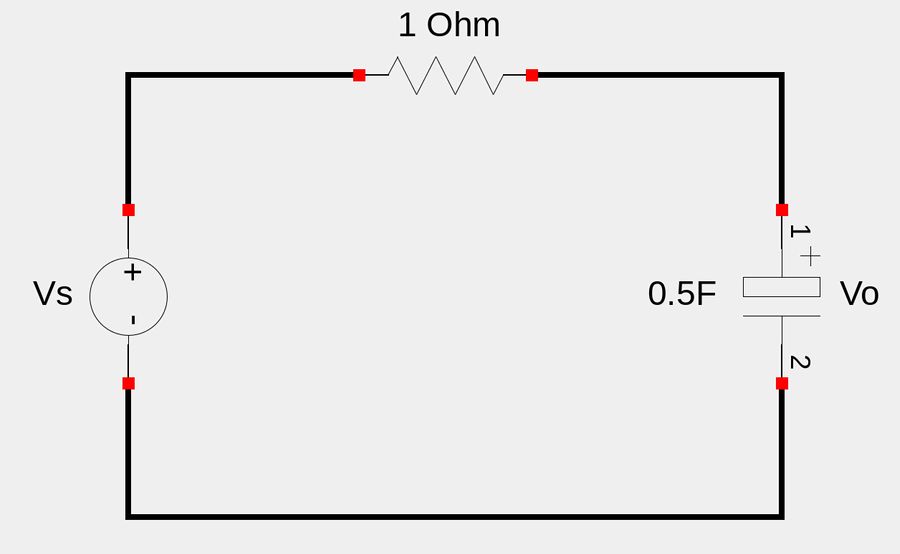
Use convolution to determine Vo
We begin by transforming the circuit to the "s" domain. Take the Laplace transform of Vs in order to transform it from the time domain to the frequency domain: $$ v_s(t) = 10e^{-t} $$
$$ \begin{align} V_s(s) &= \mathcal{L}[v_s(t)] \\\\ &= 10 \mathcal{L}[e^{-t}] \\\\ &= 10 \Big[ \frac{1}{s+1} \Big] \\\\ \end{align} $$
$$ V_s(s) = \frac{10}{s+1} $$
Next, recall the definition for the impedance of a capacitor (defined in the Impedance/Admittance section of AC circuit analysis): $$ \mathbb{Z}_C = \frac{-j}{\omega C} =\frac{1}{j\omega C} $$ and since: $$ j\omega = s $$ ...we have: $$ \mathbb{Z}_C = \frac{1}{s C} $$ Therefore, for the circuit shown above: $$ \mathbb{Z}_C = \frac{1}{0.5s} $$
$$ \mathbb{Z}_C = \frac{2}{s} $$
Now redraw the circuit using the values we just determined:
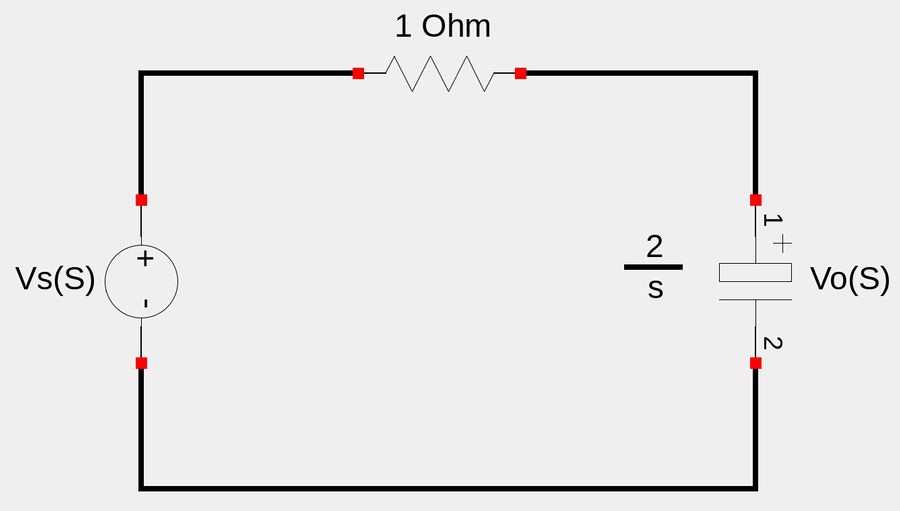
Derive an expression for the output voltage in the s-domain:
Using the principle of voltage division, we have: $$ \begin{align} V_o(s) &= \frac{\frac{2}{s}}{1+\frac{2}{s}} V_s(s) \\\\ &= \frac{\frac{2}{s}}{\frac{s+2}{s}} V_s(s) \\\\ &= \frac{2}{\cancel{s}} \Big( \frac{\cancel{s}}{s+2} \Big) V_s(s) \\\\ V_o(s) &= \frac{2}{s+2} V_s(s) \qquad, (Eqn\;1) \end{align} $$
Derive an expression for the impulse response in the s-domain:
The impulse response of the circuit is defined as: $$ H(s) = \frac{V_o(s)}{V_s(s)} $$ Recalling equation #1: $$ V_o(s) = \frac{2}{s+2} V_s(s) $$ By rearranging it we get: $$ \frac{V_o(s)}{V_s(s)} = \frac{2}{s+2} $$ Therefore: $$ H(s) = \frac{2}{s+2} $$
Convert the impulse response from the s-domain to the time domain:
We do this by taking the inverse Laplace transform of H(s): $$ \begin{align} h(t) &= \mathcal{L^{-1}}[H(s)] \\\\ &= \mathcal{L^{-1}} \Big[ \frac{2}{s+2} \Big] \\\\ \end{align} $$
$$ h(t) = 2e^{-2t} $$
Use the convolution integral to get Vo(t):
The work done above has given us time-domain expressions for the impulse response, h(t), and input voltage, Vs(t). By convoluting these two expressions, we will obtain the output voltage, Vo(t), in the time domain. Recalling the definition of the convolution integral, we proceed as follows:
We do this by taking the inverse Laplace transform of H(s): $$ \begin{align} v_o(t) &= h(t) * v_s(t) \\\\ &= \int_{0}^{t} h(\tau) v_s(t-\tau) \; d\tau \\\\ &= \int_{0}^{t} (2e^{-2\tau})(10e^{-(t-\tau)}) \; d\tau \\\\ &= 20 \int_{0}^{t} (e^{-2\tau} e^{-t} e^\tau) \; d\tau \\\\ &= 20e^{-t} \int_{0}^{t} e^{-\tau} \; d\tau \\\\ &= 20e^{-t} \Big[ \frac{1}{-1} e^{-\tau} \Big] \Big|^t_{0} \\\\ &= -20e^{-t} [e^{-t} - 1] \\\\ \end{align} $$
$$ v_o(t) = 20[e^{-t} - e^{-2t}] \; V $$
Verify the result:
We can verify this answer by performing the equivalent operation in the s-domain. We start at the point above where we used voltage division to get: $$ V_o(s) = \frac{2}{s+2} V_s(s) $$ At the beginning of this page we also determined that: $$ V_s(s) = \frac{10}{s+1} $$ Therefore... $$ V_o(s) = \frac{2}{s+2} \Big( \frac{10}{s+1} \Big) = \frac{20}{(s+1)(s+2)} $$ In order to get the output voltage in the time domain, we take the inverse Laplace transform of the above expression: $$ \begin{align} v_o(t) &= \mathcal{L^{-1}}[V_o(s)] \\\\ v_o(t) &= \mathcal{L^{-1}} \Big[ \frac{20}{(s+1)(s+2)} \Big] \end{align} $$
We expand the fractional term using partial fraction decomposition: $$ \begin{align} \frac{20}{(s+1)(s+2)} &= \frac{A}{s+2} + \frac{B}{s+1} \\\\ 20 &= A(s+1) + B(s+2) \\\\ 20 &= As + A + Bs + 2B \\\\ 20 &= s(A+B) + A + 2B \\\\ \end{align} $$ We now equate terms on both sides of the equation. For the "s" terms: $$ A+B=0 $$ $$ A=-B \qquad,\;equation\;2 $$ For the constants: $$ A+2B=20 \qquad,\;equation\;3 $$ Substitute equation #2 into equation #3: $$ -B+2B=20 $$ $$ B=20 \qquad,\;equation\;4 $$ Substitute equation #4 into equation #2: $$ A=-20 $$ Therefore: $$ \frac{20}{(s+1)(s+2)} = \frac{20}{s+1} - \frac{20}{s+2} $$ We now pick up where we left off:
$$ \begin{align} v_o(t) &= \mathcal{L^{-1}} \Big[ \frac{20}{s+1} - \frac{20}{s+2} \Big] \\\\ &= 20\mathcal{L^{-1}} \Big[ \frac{1}{s+1} \Big] - 20\mathcal{L^{-1}} \Big[ \frac{1}{s+2} \Big] \\\\ &= 20e^{-t}-20e^{-2t} \end{align} $$
$$ v_o(t) = 20[e^{-t} - e^{-2t}] \; V $$ This agrees with our answer above.
In the next example, we will see how the convolution integral can be used to determine the inverse Laplace transform of a function thereby transforming from the frequency domain to the time domain.
Continue on to example problem #4 (involving the inverse Laplace transform)...
