Instantaneous Power:
Instantaneous power is the product of the instantaneous voltage across a circuit element and the instantaneous current through it: $$ p(t) = v(t) \; i(t) $$ The above expression defines power at any instant of time and is the rate at which an element absorbs energy (in watts). If the circuit is driven by a sinusoidal (AC) source then voltage and current can be defined by: $$ v(t) = V_m\cos (\omega t + \theta_v ) $$ $$ i(t) = I_m\cos(\omega t + \theta_i) $$ ...where Vm and Im are the magnitudes of the voltage and current sinusoids. Our definition for instantaneous power now becomes: $$ p(t) = V_m I_m \cos (\omega t + \theta_v ) \cos (\omega t + \theta_i ) \qquad,(I) $$
Recall the following trigonometric identity: $$ \cos A \cos B = \frac{\cos (A+B) + \cos (A-B)}{2} $$ ...and apply it to expression #1:
$$ p(t) = $$ $$ \;\; V_m I_m \Big[ \frac{\cos (\omega t + \theta_v + \omega t + \theta_i) + \cos (\omega t + \theta_v - \omega t - \theta_i)}{2} \Big] $$ $$ = \frac{V_m I_m}{2} [\cos (2\omega t + \theta_v + \theta_i) + \cos (\theta_v - \theta_i)] $$
$$ p(t) = \Big[ \frac{1}{2} V_m I_m \cos (\theta_v - \theta_i) \Big] $$ $$ \qquad + \Big[ \frac{1}{2} V_m I_m \cos (2\omega t + \theta_v + \theta_i) \Big] \;\;\;\; , (II)$$
Instantaneous power has two components:
From equation two we see that the 1st bracketed term is constant (time-independent). It's value depends on the phase-difference between voltage and current. The second bracketed term is a sinusoidal function that is time dependent with an angular frequency of 2*omega. This angular frequency is twice that of the voltage and current. If we were to plot our function for p(t) found in equation #2 it would look like the following:
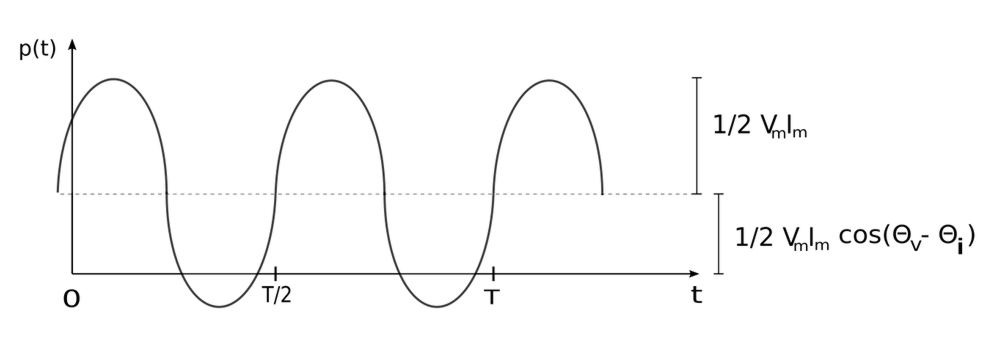
Let's try to make sense of this graph. Recall that we defined voltage and current as: $$ v(t) = V_m\cos (\omega t + \theta_v ) $$ $$ i(t) = I_m\cos(\omega t + \theta_i) $$ and that angular frequency is defined as: $$ \omega = 2\pi f $$ ...so frequency is defined as: $$ f = \frac{\omega}{2\pi} \qquad,(3)$$ Remember that Period (T) is the inverse of frequency, so: $$ T = \frac{2\pi}{\omega} \qquad,(4) $$ Now consider our expression for instantaneous power: $$ p(t) = \Big[ \frac{1}{2} V_m I_m \cos (\theta_v - \theta_i) \Big] $$ $$ \qquad + \Big[ \frac{1}{2} V_m I_m \cos (2\omega t + \theta_v + \theta_i) \Big] $$ The angular frequency for p(t) is twice the angular frequency for voltage and current and is equal to its own frequency times 2pi: $$ \omega_p = 2\omega = 2\pi f_p $$ So the frequency of p(t) is: $$ f_p = \frac{\omega}{\pi} $$ ...and if we compare this to the frequency of voltage and current (expression #3) we see that the frequency of instantaneous power is twice that of voltage and current. Furthermore, the period of our instantaneous power function is defined as: $$ T_p = \frac{1}{f_p} = \frac{\pi}{\omega} $$ ...which is half the value of expression #4. Therefore the period for instantaneous power is: $$ T_p = \frac{T}{2} $$ ...as seen in the graph.
We also notice that p(t) is positive for some parts of its cycle and negative for others.
When p(t) is positive:
Power is absorbed by the circuit
When p(t) is negative:
Power is absorbed by the source (transferred from the circuit to the source). This is possible due to the storage elements in the circuit (capacitors, inductors)
Average Power:
Since instantaneous power changes with time, it is difficult to measure. This is where average power comes in. Average power is defined as the average of the instantaneous power over one period. (also measure in watts.) As a refresher, let's visit the definition of the average of a periodic function (defined below:)
The average of a periodic function is defined as: $$ \bar{f} = \frac{1}{t_b - t_a} \int_{t_a}^{t_b} f(t)dt $$ ...where: $$ \bar{f} = avg. \; value \; function $$ If we have a period (T) defined in seconds then we get: $$ \bar{f} = \frac{1}{T} \int_0^T f(t)dt $$
The period of our expression for instantaneous power (equation II) is: $$ T = \frac{\pi}{\omega} $$ We can now define average power as: $$ \bar{p} = \frac{1}{\frac{\pi}{\omega}} \int_0^{\frac{\pi}{\omega}} \Big[ \frac{1}{2} V_m I_m \cos (\theta_v - \theta_i) $$ $$ \qquad + \frac{1}{2} V_m I_m \cos (2\omega t + \theta_v + \theta_i) \Big] dt $$ $$ \bar{p} = \frac{\omega}{\pi} \int_0^{\frac{\pi}{\omega}} \Big[ \frac{1}{2} V_m I_m \cos (\theta_v - \theta_i) \Big] dt $$ $$ \qquad + \frac{\omega}{\pi} \int_0^{\frac{\pi}{\omega}} \Big[ \frac{1}{2} V_m I_m \cos (2\omega t + \theta_v + \theta_i) \Big] dt $$ In regards to the 2nd integral, we know that the average value of a sinusoid over its period is zero. Therefore we evaluate the first integral only and our expression now becomes: $$ \bar{p} = \frac{\omega}{\pi}\Big( \frac{1}{2} \Big) t \; V_m I_m \cos(\theta_v - \theta_i) \Big|_0^{\frac{\pi}{\omega}} $$ $$ = \frac{\omega}{2\pi} \Big( \frac{\pi}{\omega} \; \Big) V_m I_m \cos(\theta_v - \theta_i) - 0 $$ After evaluating the above expression we get
Average Power:
$$ \bar{p} = \frac{1}{2} V_m I_m \cos(\theta_v - \theta_i) \qquad ,Eqn \; 5$$ Note that average power is not time-dependent.
Average power can be determined when voltage and current are both expressed in the time-domain or when they are expressed in the phasor/frequency domain.
Using Phasors to Calculate Average Power:
Recall the definition of phasor voltage and current: $$ \mathbb{V} = V_m \angle \theta_v $$ $$ \mathbb{I} = I_m \angle \theta_i $$ ...where Vm and Im are the magnitudes of the voltage and current sinusoids. Consider what happens when we expand the following expression: $$ \frac{1}{2} \mathbb{V} \mathbb{I} * $$
Recall the definition of the complex conjugate of an imaginary number 'Z' expressed in phasor form: $$ \mathbb{Z}* = (x-jy) = r \angle (-\theta) $$ Which allows us to expand our above expression in the following manner:
$$ \frac{1}{2} \mathbb{V} \mathbb{I} * = \frac{1}{2}(V_m\angle \theta_v)(I_m \angle (-\theta_i)) $$ $$ = \frac{1}{2} V_m I_m \angle (\theta_v - \theta_i) $$ $$ = \frac{1}{2} V_m I_m e^{j(\theta_v - \theta_i)} $$
Recall Euhler's Identity: $$ e^{j\theta} = \cos \theta + j\sin \theta $$ ... and apply it to the above expression:
$$ \frac{1}{2} \mathbb{V} \mathbb{I} * = \frac{1}{2} V_m I_m [\cos (\theta_v - \theta_i) + j\sin (\theta_v - \theta_i)] $$ $$ \frac{1}{2} \mathbb{V} \mathbb{I} * = \Big[ \frac{1}{2} V_m I_m \cos(\theta_v - \theta_i) \Big] $$ $$ \qquad + j \Big[ \frac{1}{2} V_m I_m \sin(\theta_v - \theta_i) \Big]$$ You may recognize the real part of the above complex number as being the same as our above-derived expression for average power (equation #5). Therefore, we now have an expression for average power in terms of phasors:
Special Case (voltage and current are in-phase):
When voltage and current are in-phase: $$ \theta_v = \theta_i $$ ...which means that equation 6 becomes: $$ \bar{p} = \frac{1}{2} V_m I_m \qquad,Eqn \; 7$$ With no phase-shift, the circuit is said to be "purely resistive" and: $$ V_m = I_m R $$ Therefore, equation #7 can be rewritten as: $$ \bar{p} = \frac{1}{2} I_m^2 R $$ Expressed in phasor form: $$ \bar{p} = \frac{1}{2} |\mathbb{I}|^2 R $$ Utilizing the property of the absolute square of a complex number: $$ \bar{p} = \frac{1}{2} \mathbb{I} \; \mathbb{I*} \; R $$
So, for a purely resistive circuit: $$ \theta_v = \theta_i $$ and: $$ \bar{p} = \frac{1}{2} V_m I_m = \frac{1}{2} I_m^2 R = \frac{1}{2} \mathbb{I} \; \mathbb{I*} \; R $$ A purely resistive circuit absorbs power at all times.
Special Case (voltage and current are 90 degrees out of phase):
When: $$ \theta_v - \theta_i = \pm 90^{\circ} $$ ...the circuit is "purely reactive" and equation #6 becomes: $$ \bar{p} = \frac{1}{2} V_m I_m \cos(\pm 90^{\circ}) $$ $$ \bar{p} = 0 $$
So for a purely reactive circuit: $$ \theta_v - \theta_i = \pm 90^{\circ} $$ $$ \bar{p} = 0 $$ A purely reactive circuit absorbs no power.
Let's look at an example problem involving average power:
Continue on to Average power (example problem)...
