For the following circuit, determine the power absorbed by the 50 ohm resistor:
Let: $$ i_s = 6\cos (10^3t) \; A $$
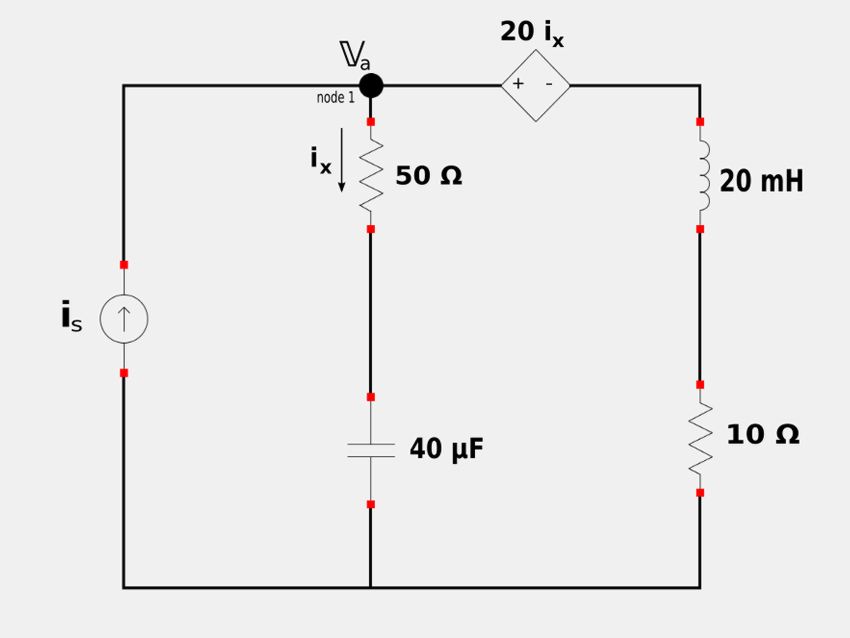
Start by converting the circuit elements to the frequency domain : $$ i_s = 6\cos (10^3t) = 6\angle 0^{\circ} $$ $$ \mathbb{Z}_c = \frac{-j}{1,000(40\times 10^{-6})} = -j25 \; \Omega $$ $$ \mathbb{Z}_L = j1,000 (20\times 10^{-3}) = j20 \; \Omega$$ Also, note that: $$ \mathbb{I}_x = \frac{\mathbb{V}_a}{50-j25} = 0.0179\mathbb{V}_a \angle 26.57^{\circ} , \qquad(Eqn \; 1) $$
Apply Kirchhoff's Current Law (KCL) to node 1:
$$ \frac{\mathbb{V}_a}{50-j25} + \frac{\mathbb{V}_a - 20\mathbb{I}_x}{10+j20} = 6 $$ $$ \frac{\mathbb{V}_a}{55.9\angle (-26.57^{\circ})} + \frac{\mathbb{V}_a}{22.36 \angle 63.44^{\circ}} - \Big( \frac{20}{22.36 \angle 63.44^{\circ}} \Big)\mathbb{I}_x = 6$$ $$ 0.0179\mathbb{V}_a \angle 26.57^{\circ} + 0.0447\mathbb{V}_a \angle (-63.44^{\circ}) - [0.8944\angle (-63.44^{\circ}) ]\mathbb{I}_x = 6$$ Summing the two Va terms and substituting our value for Ix (found in eqn #1) gives us: $$ 0.0482\mathbb{V}_a \angle(-41.62^{\circ}) - [0.8944\angle (-63.44^{\circ})][0.0179\mathbb{V}_a \angle 26.57^{\circ}] = 6 $$ $$ 0.0482\mathbb{V}_a \angle(-41.62^{\circ}) - 0.016\mathbb{V}_a \angle (-36.87^{\circ}) = 6 $$ $$ 0.0323\mathbb{V}_a \angle (-43.97^{\circ}) = 6 $$ $$ \mathbb{V}_a = 185.9 \angle 43.97^{\circ} $$
Use our determined value for Va to solve for Ix:
From equation #1: $$ \mathbb{I}_x = 0.0179\mathbb{V}_a \angle 26.57^{\circ} $$ Substituting our above-determined value for Va: $$ \mathbb{I}_x = (0.0179 \angle 26.57^{\circ})(185.9 \angle 43.97^{\circ}) $$ $$ \mathbb{I}_x = 3.328 \angle 70.54^{\circ} \; A $$
Determine the avg. power of the 50 ohm resistor:
Recognize that the resistor represents a purely resistive load. From the Intro to instantaneous and average power page, we learned that the power for such a case is found using the following expression: $$ \bar{p} = \frac{1}{2} \mathbb{I} \; \mathbb{I*} \; R $$ where: $$ \mathbb{I}* = i_x \angle (-\theta_{i_x}) $$ So: $$ \bar{p}_{50\Omega} = \frac{1}{2} [3.328 \angle 70.54^{\circ}][3.328 \angle (-70.54^{\circ})]\; 50 $$
$$ \bar{p}_{50\Omega} = 276.9 \; W $$
