Calculate the RMS current and average power delivered to a 12 ohm resistor by the following periodic, triangle waveform:
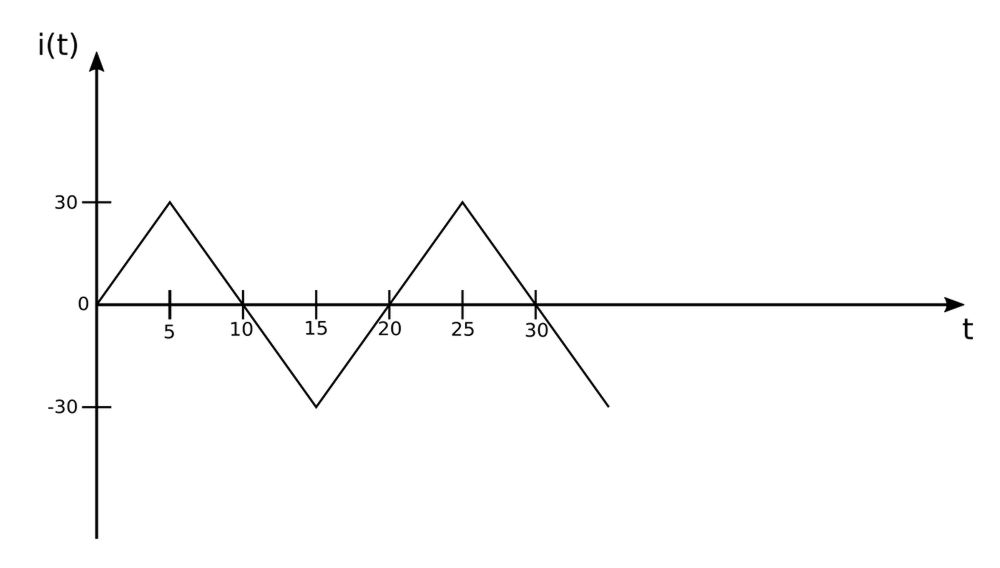
Derive an expression for the signal over one period
We starting by noticing that the period of this signal is : $$ T = 20 $$ We now want to come up with an expression that defines the waveform over the course of one period. If we look at the waveform starting at t=5 going till t=15 we see that is the graph of the line i=-6t (slope = -6) shifted to the right 10 units. We express this using the simple equation of a line: $$ i(t) = -6(t-10) $$ $$ i(t) = -6t + 60 \qquad, 5 \lt t \lt 15 $$ If we look at the waveform from t=15 till t=25, we see that it is the graph of the line i=6t (slope=6) shifted 20 units to the right. Therefore we have: $$ i(t) = 6(t-20)) $$ $$ i(t) = 6t-120 \qquad,15 \lt t \lt 25 $$ We now have the following piece-wise expression for i(t) over one period: $$ i(t) = \left\{ \begin{array}{ll} -6t+60 & 5 \lt t \lt 15 \\ 6t-120 & 15 \lt t \lt 25 \end{array} \right. $$
Calculate RMS current:
Recall the generic expression (derived in the previous page)for the RMS value of a periodic function x(t): $$ X_{rms} = \sqrt{\frac{1}{T} \int_0^T x^2 \; dt} $$ ...and apply it to our signal: $$ I_{rms} = \sqrt{\frac{1}{T} \int_0^T i^2 \; dt} $$ Since our waveform is expressed as a piece-wise function containing two parts, we will be evaluating two integrals (one for each half of the period): $$ I_{rms} = \sqrt{\frac{1}{20} \Big[ \int_5^{15} (-6t+60)^2 \; dt + \int_{15}^{25} (6t-120)^2 \Big] \; dt} $$
$$ = \sqrt{\frac{1}{20} \Big[ \int_5^{15} 36t^2-720t+3600 \; dt + \int_{15}^{25} 36t^2-1440t+14400 \Big] \; dt} $$ $$ = \sqrt{\frac{1}{20} \Big[ (12t^3-360t^2+3600t)\Big|_5^{15} + (12t^3-720t^2+14400t)\Big|_{15}^{25} \Big] } $$
$$ =\sqrt{\frac{1}{20} \Big[ (13500-10500) + (97500-94500) \Big]} $$ $$ =\sqrt{\frac{1}{20}(6000)} $$
$$ I_{rms} = 17.32 \;A $$
Calculate power delivered to a 12 ohm resistor:
Recall that towards the end of the previous page we derived the following expression for the RMS power delivered to a purely resistive load: $$ P_{rms} = I_{rms}^2 R $$ In our example problem here we get: $$ P_{rms} = (17.32)^2(12) $$ So for a 12 ohm resistor, the power is:
$$ P_{rms} = (3.6 \times 10^3 ) \; W = 3.6 \; kW $$
