Mesh analysis is based off of Kirchoff's Voltage Law (KVL). Since KVL is valid for AC circuits, we can therefore use mesh analysis to analyze these same circuits. The simplest way is to begin with an example problem.

For the following circuit, determine the phasor current (Io) using mesh analysis:

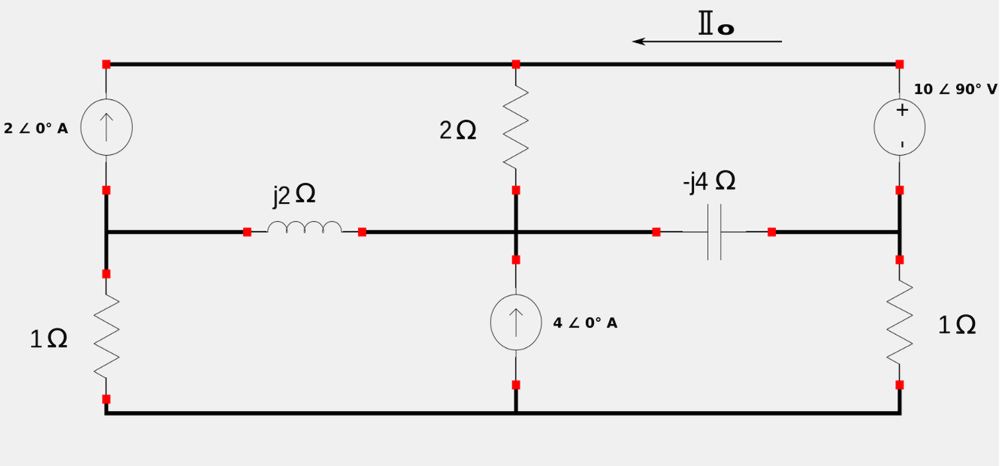
Mesh analysis circuit

Notice that in the above circuit the bottom two meshes have a common current source. In such a case we proceed in a similar manner as with a DC circuit that has two meshes with a common current source and create a "super-mesh" by eliminating the current source but retaining the individual mesh currents. The following circuit shows our super mesh as well as the 4 individual mesh currents:

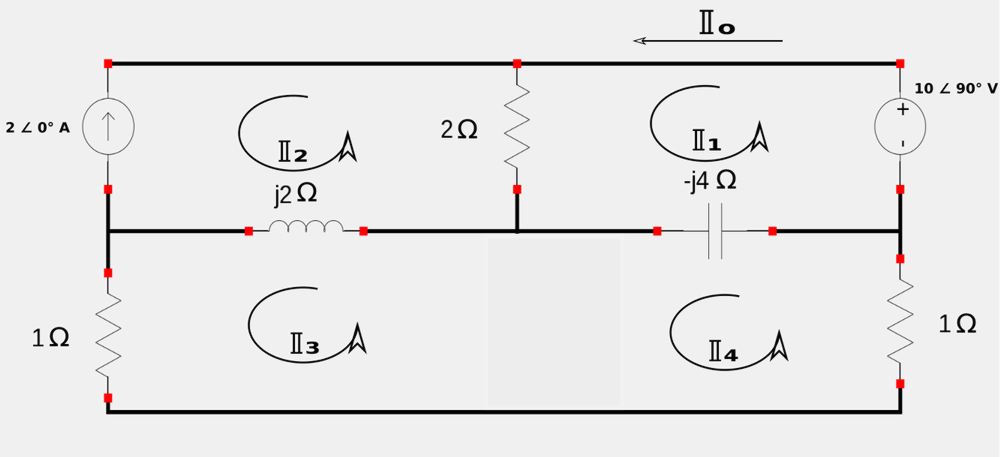
Mesh analysis circuit with a super-mesh

Apply KVL inside the super-mesh:

$$ \mathbb{I}_3 + \mathbb{I}_4 - j4(\mathbb{I}4 - \mathbb{I}_1) + j2(\mathbb{I}_3 - \mathbb{I}_2) = 0 $$ $$ \mathbb{I}_3 + \mathbb{I}_4 - j4\mathbb{I}_4 + j4\mathbb{I}_1 + j2\mathbb{I}_3 - j2\mathbb{I}_2 = 0 $$ $$ j4\mathbb{I}_1 - j2\mathbb{I}_2 + \mathbb{I}_3(1+j2) + \mathbb{I}_4(1-j4) = 0 \qquad,(Eqn \; 1) $$

However, we can also create an equation out of meshes 3/4 and their common current source: $$ \mathbb{I}_3 - \mathbb{I}_4 = 4 $$ $$ \mathbb{I}_3 = 4 + \mathbb{I}_4 $$ Now go ahead and substitute this expression for phasor current II3 into equation #1:

Equation #1 now becomes: $$ j4\mathbb{I}_1 - j2\mathbb{I}_2 + (4 + \mathbb{I}_4)(1+j2) + \mathbb{I}_4(1-j4) = 0 $$ $$ j4\mathbb{I}_1 - j2\mathbb{I}_2 + 4 + j8 + \mathbb{I}_4 + j2\mathbb{I}_4 + \mathbb{I}_4(1-j4) = 0 $$ $$ j4\mathbb{I}_1 - j2\mathbb{I}_2 + \mathbb{I}_4(1-j4+1+j2) = -4-j8 $$ $$ j4\mathbb{I}_1 - j2\mathbb{I}_2 + \mathbb{I}_4(2-j2) = -4-j8 $$ If we convert the above equation (containing complex numbers) from rectangular to polar form we get: $$ 4\mathbb{I}_1 \angle 90^{\circ} + 2\mathbb{I}_2 \angle (-90^{\circ}) + 2.828\mathbb{I}_4 \angle (-45^{\circ}) = 8.944 \angle 243.4^{\circ} \;\;\;\;,(Eqn \; 2) $$ However, notice that in mesh #2 we have: $$ \mathbb{I}_2 = -2 $$ ...and if we substitute this into equation #2 and bring the result to the right side of the equation, we get: $$ 4\mathbb{I}_1 \angle 90^{\circ} + 2(-2) \angle (-90^{\circ}) + 2.828\mathbb{I}_4 \angle (-45^{\circ})= 8.944 \angle 243.4^{\circ} $$ $$ 4\mathbb{I}_1 \angle 90^{\circ} + 2.828\mathbb{I}_4 \angle (-45^{\circ}) = 8.944 \angle 243.4^{\circ} + 4 \angle (-90^{\circ}) $$ Working only the right side of the above equation (in rectangular form): $$ "\qquad \qquad \qquad " = -4-j8-j4 $$ $$ "\qquad \qquad \qquad " = -4-j12 $$ ...gives us the following (after converting back to polar form):

$$ 4\mathbb{I}_1 \angle 90^{\circ} + 2.828\mathbb{I}_4 \angle (-45^{\circ}) = 12.65 \angle 251.6^{\circ} \qquad,(Eqn \; 3)$$

Apply KVL inside mesh #1:

$$ -j4(\mathbb{I}_1 - \mathbb{I}_4) - 10 \angle 90^{\circ} + 2(\mathbb{I}_1 - \mathbb{I}_2) = 0 $$ Recall that: $$ \mathbb{I}_2 = -2 $$ and substitute it into the above equation to get: $$ -j4\mathbb{I}_1 + j4\mathbb{I}_4 + 2\mathbb{I}_1 + 4 = 10 \angle 90^{\circ} $$ $$ \mathbb{I}_1(2-j4) + j4\mathbb{I}_4 = 10 \angle 90^{\circ} - 4 $$ $$ \mathbb{I}_1(2-j4) + j4\mathbb{I}_4 = -4 + 10j $$ Converting to polar form gives us:

$$ 4.472\mathbb{I}_1 \angle(-63.43^{\circ}) + 4\mathbb{I}_4 \angle 90^{\circ} = 10.77 \angle 111.8^{\circ} \qquad, (Eqn \; 4)$$

Solve system of equations for equations 3/4

While several techniques can be used to solve the equations, we will use Cramer's Rule.

Create an augmented matrix of coefficients from our system of equations:

$$ \begin{pmatrix} 4 \angle 90^{\circ}&2.828 \angle (-45^{\circ})&12.65 \angle 251.6^{\circ}\\ 4.472\angle (-63.43^{\circ})&4 \angle 90^{\circ}&10.77 \angle 111.8^{\circ}\\ \end{pmatrix} $$

Find the determinant of the non-augmented matrix of coefficients:

$$ D = \begin{vmatrix} 4 \angle 90^{\circ}&2.828 \angle (-45^{\circ})\\ 4.472\angle (-63.43^{\circ})&4 \angle 90^{\circ}\\ \end{vmatrix} $$ $$ = (4 \angle 90^{\circ})(4 \angle 90^{\circ}) - \Big( 4.472\angle (-63.43^{\circ}) \Big) \Big( 2.828 \angle (-45^{\circ}) \Big) $$ $$ = 16 \angle 180^{\circ} - 12.65 \angle (-108.4^{\circ}) $$ $$ -16 + 3.993 + j12 $$ $$ = -12.01 + j12 $$

$$ D = 16.98 \angle 135^{\circ} $$

Create a matrix that consists of the non-augmented matrix of coefficients with its 1st column replaced by the 3rd column of the augmented matrix of coefficients:

...and proceed to find the determinant: $$ D_{\mathbb{I}_1} = \begin{vmatrix} 12.65 \angle 251.6^{\circ}&2.828 \angle (-45^{\circ})\\ 10.77 \angle 111.8^{\circ}&4 \angle 90^{\circ}\\ \end{vmatrix} $$

$$ D_{\mathbb{I}_1} = (12.65 \angle 251.6^{\circ})(4 \angle 90^{\circ}) - (10.77 \angle 111.8^{\circ})(2.828 \angle (-45^{\circ})) $$ $$ = 50.6 \angle 341.6^{\circ} - 30.46 \angle 66.8^{\circ} $$ $$ = 48.01 - j15.97 - 12 - j28 $$ $$ 36.01 - j43.97 $$

$$ D_{\mathbb{I}_1} = 56.83 \angle (-50.68^{\circ}) $$

From the original two circuit schematics, note that: $$ \mathbb{I}_1 = \mathbb{I}_o $$ ...and recall that Cramer's Rule states the following: $$ \mathbb{I}_1 = \frac{D_{\mathbb{I}_1}}{D} $$ Therefore: $$ \mathbb{I}_o = \frac{D_{\mathbb{I}_1}}{D} $$ $$ = \frac{56.83 \angle (-50.68^{\circ})}{16.98 \angle 135^{\circ}} $$ $$ = \frac{56.83}{16.98} \angle (-50.68^{\circ} - 135^{\circ}) $$

$$ \mathbb{I}_o = 3.347 \angle (-185.7^{\circ}) = 3.347 \angle 174.3^{\circ} $$