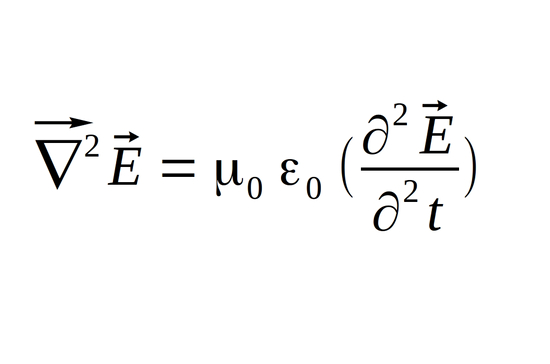The following derivations make use of "THE" Identity shown below: (not proven here)
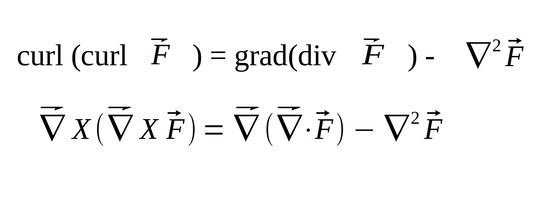
...as well as Maxwell's Equations for a source-free region:
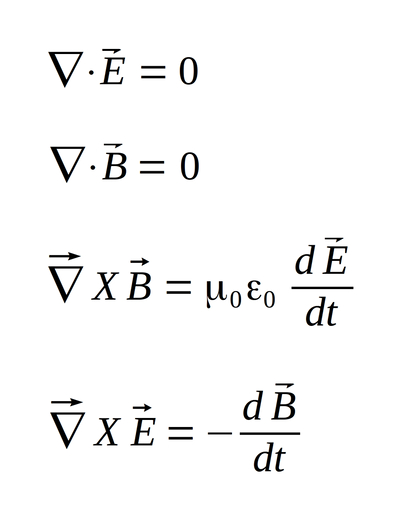
Electromagnetic Wave Equation for Magnetic Field
Beginning with Maxwell's 3rd equation for a source free region, we take the curl of both sides:
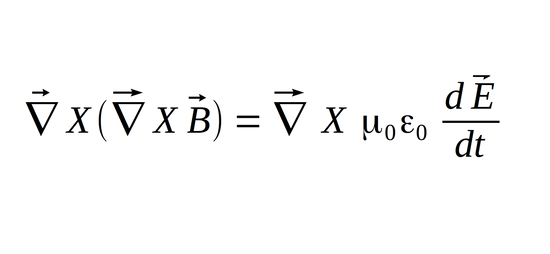
...and using "THE" Identity, we rewrite the left side of the equation accordingly. We also pull any scalars outside of our cross product on the right side of the equation:
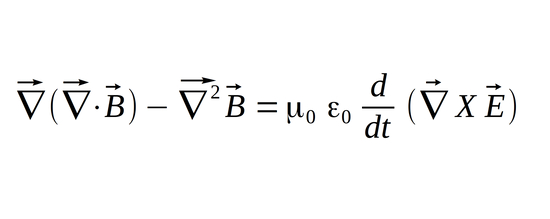
Recalling Maxwell's 2nd and 4th equations for a source-free region:
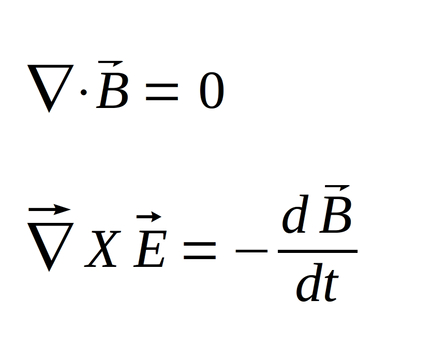
...we make the appropriate substitutions which leaves us with:
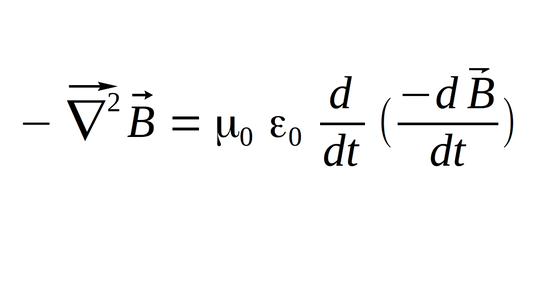
The negative signs cancel and the derivative terms on the right side become the 2nd derivative of magnetic field with respect to time. (Remember mu-naught and epsilon-naught are constants) The final result is the:
Wave Equation for Magnetic Field:
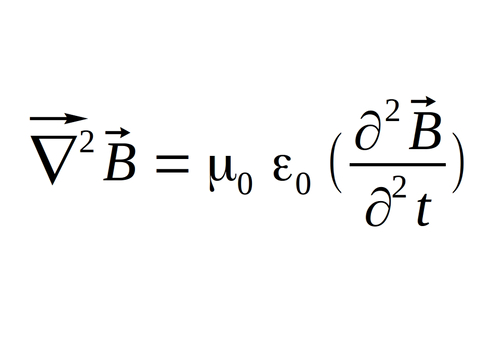
Electromagnetic Wave Equation for Electric Field
We begin with Maxwells' 4th equation for a source-free region and take the curl of both sides:
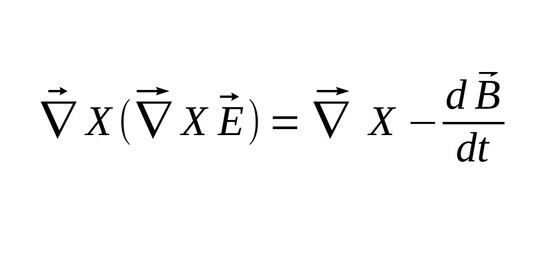
Once again we use "THE" Identity to rewrite the left side of the equation:
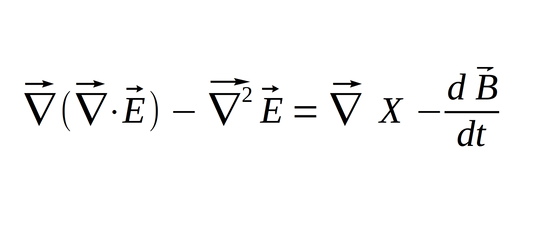
...and pull the derivative notation outside of the cross product on the right side of the equation:
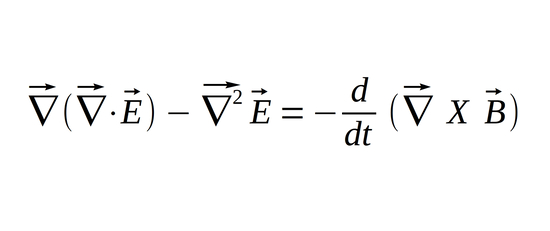
We recall Maxwell's 1st and 3rd equations for a source-free region
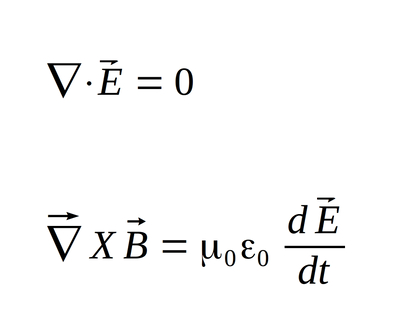
...and after making the appropriate substitutions we arrive at the following:
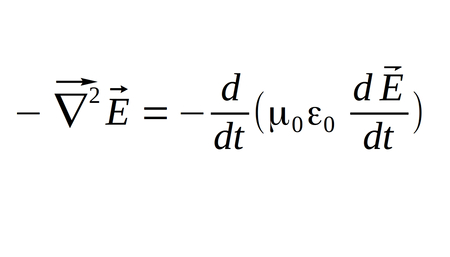
The negative signs cancel and the derivative terms on the right side become the 2nd derivative of electric field with respect to time. (Remember mu-naught and epsilon-naught are constants). The final result is the:
Wave Equation for Electric Field: