We will prove that for a given electromagnetic wave, neither the electric nor magnetic fields have components in the direction of the other. (electric and magnetic field are mutually orthogonal)
We will consider an electromagnetic wave propagating in the positive z-direction and define the electric field as being in the positive x-direction (shown below in component form):
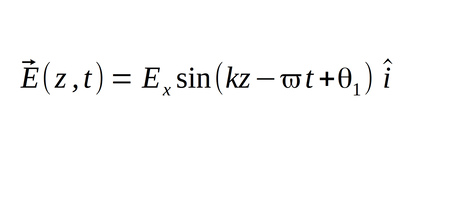
and the magnetic field shown below in component form:
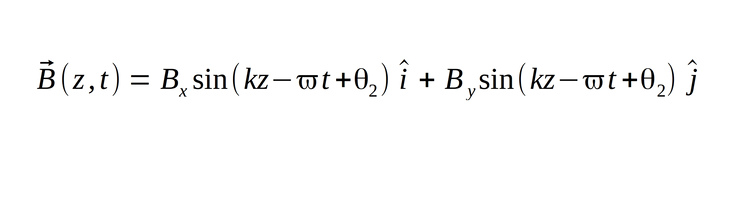
Also, recall that we have already proven that neither the electric nor magnetic field have any components in the direction of wave propagation (z-direction in this case). Therefore, there is no z-component for magnetic field. However, there potentially exists (as of the moment) a component of B in the direction of E (the x-direction). We aim to prove that such an occurrence is not possible.
We begin by taking the curl of the electric field:
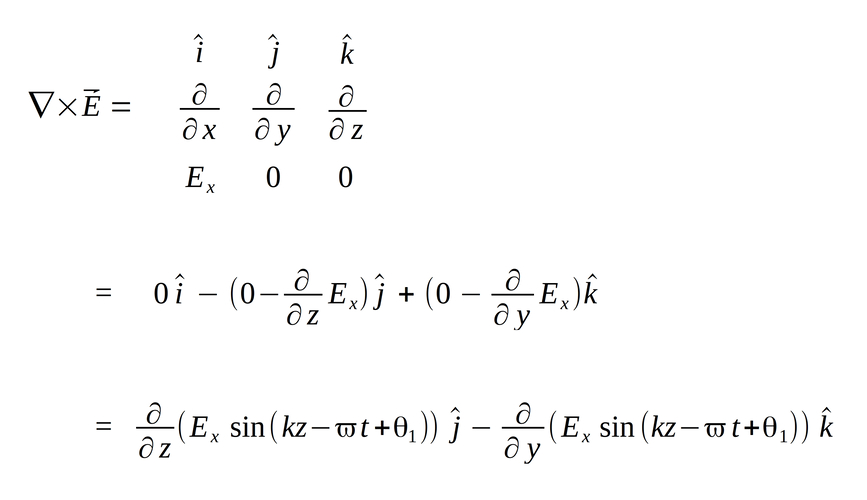
We also notice that since there is no y term in the above result of our cross-product, the k-component becomes zero and we are left with:
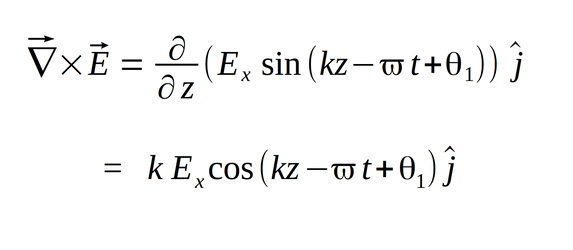
We also recall Maxwell's 4th equation for a source-free region...:
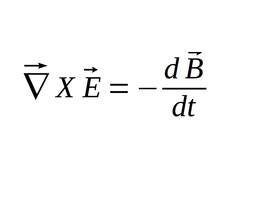
...which we equate to the resulting curl of the electric field:
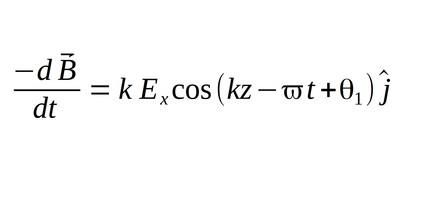
Now let's find the negative derivative of the magnetic field with respect to time:
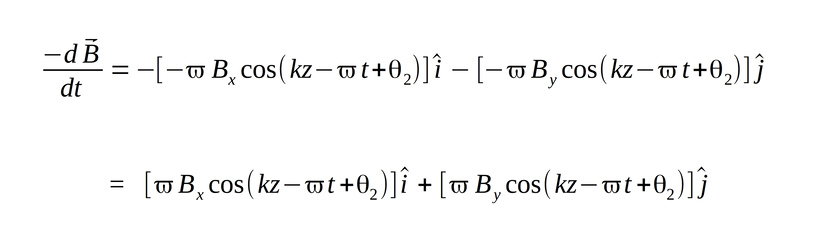
...and plug it into our equation:
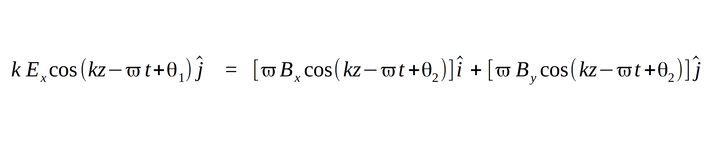
We now recognize that for the above statement to be true, the i component on the right hand side of the equation must be zero for all values of z and t. The only way for this to be possible is if the magnetic field (B) has no component in the direction of the x-axis (B sub x = 0). Therefore, the magnetic field (B) can have no component in the direction of the electric field (E) and hence E and B are mutually orthogonal.
With the i component of the above equation reduced to zero we are left with the following:
(equation 1)
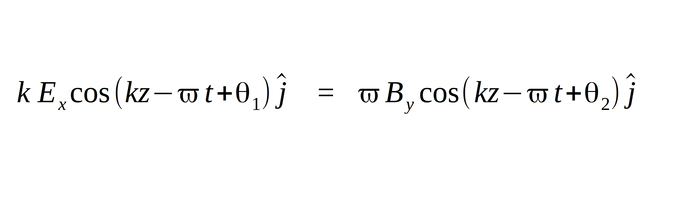
This mathematical statement allows for some interesting observations regarding the electric and magnetic field of an electromagnetic wave:
1) phase angle:
Given the above derived relationship, we first notice that the following must be true:
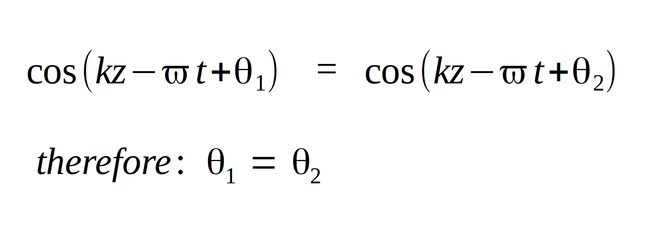
This tells us that both the electric and magnetic fields have the same phase constants and therefore they are oscillating in phase.
2) Amplitudes:
With the above mentioned property being true, we could divide both sides of equation 1 by the cosine term and get the following:
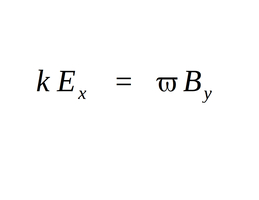
The terms on the left and right side of the equation (kE and omega B) are effectively the amplitudes of the electric and magnetic fields respectively. Being that they are equal we realize that the amplitudes of the electric and magnetic fields are also equal for an electromagnetic wave.
2) Formulating the speed of Light:
We can further manipulate the last equation in the following manner:
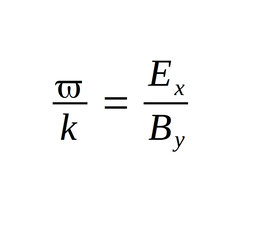
Taking note of the fact that omega divided by k is the velocity of a sinusoidal wave, as well as the fact that electromagnetic waves propagate at the speed of light, we arrive at the following relationship:

Thus we come to the additional conclusion that the magnitude of E (electric field) divided by the magnitude of B (magnetic field) is equal to the speed of light.
