Electric Field:
Consider an electromagnetic wave traveling in the positive z-direction, with the electric field function shown below (in component form):
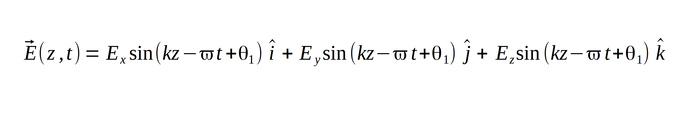
We then take the divergence (div) of the above electric field and obtain the following:
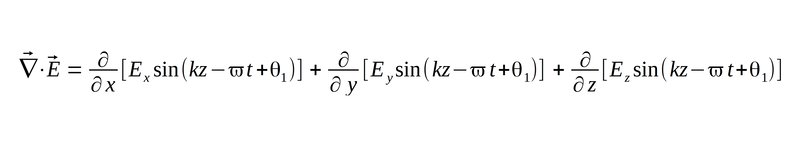
Recall Maxwell's first equation for a source-free region:
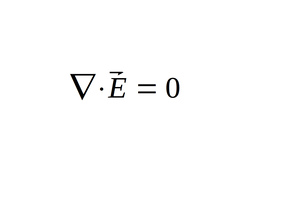
...and recognize that when taking the divergence of our electric field function, the first two terms reduce to zero being that they are constants with respect to x and y respectively. (There is no x variable in the first term and no y variable in the second term.) Therefore the left side becomes zero and the right side becomes the derivative of the 3rd term with respect to z, and we are left with:
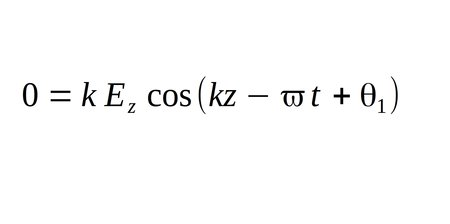
Now consider that the only scenario that would make the above statement true (and still allow for the existence of a wave) is if E sub z is equal to zero. Any other assumption that would make the above statement true would also infer the lack of a wave in the first place! Therefore if E sub z is equal to zero, then electric field (E) has no component in the direction of wave propagation (z-direction in this case.) We would arrive at the same conclusion even if the direction of wave propagation was taken to be along the x or y axis.
Magnetic Field:
Now consider the same electromagnetic wave (still traveling in the positive z direction) with the magnetic field function shown below (in component form):
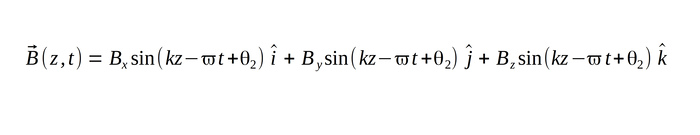
We again take the divergence (div) of the above magnetic field and obtain the following:
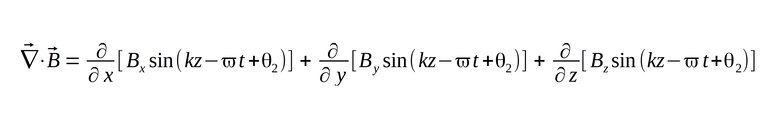
This time recall Maxwell's second equation for a source-free region:
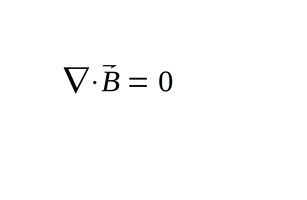
...and similar to before, we recognize that when taking the divergence of our magnetic field function, the first two terms reduce to zero being that they are constants with respect to x and y respectively. (There is no x variable in the first term and no y variable in the second term.) Therefore the left side becomes zero and the right side becomes the derivative of the 3rd term with respect to z, and we are left with:
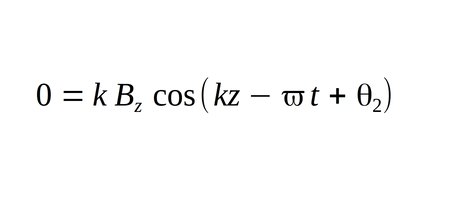
We use the same rationale here as we did with electric field and realize that the above statement can only be true (and allow for the existence of a wave) if B sub z is equal to zero. Anything else used to verify the above statement would mean no wave exists. Therefore B sub z is equal to zero, meaning that magnetic field has no component in the direction of wave propagation (z-direction in this case.) We have now proven that for an electromagnetic field, neither electric field (E) nor magnetic field (B) has a component in the direction of wave propagation (direction of wave travel).
