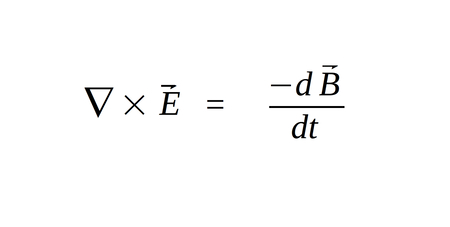We will convert Maxwell's four equations from integral form to differential form by using both the Divergence Theorem and Stokes' Theorem.

The Divergence Theorem

The Divergence Theorem relates a surface integral around a closed surface to a triple integral. In other words, it equates the flux of a vector field through a closed surface to a volume of the divergence of that same vector field.

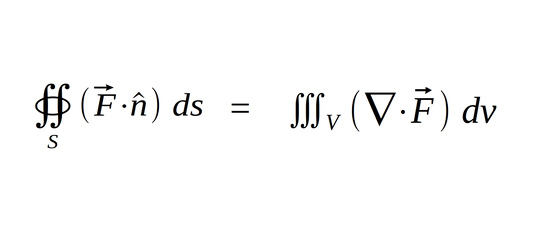
Stokes' Theorem

Stokes' theorem relates the line integral of a vector field over a closed path to the surface integral of the curl of that vector field.

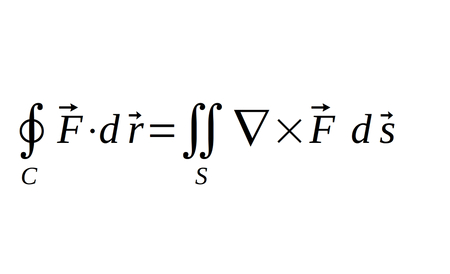
Maxwell's 1st Equation (Gauss' Law for Electric Fields)

Starting with:

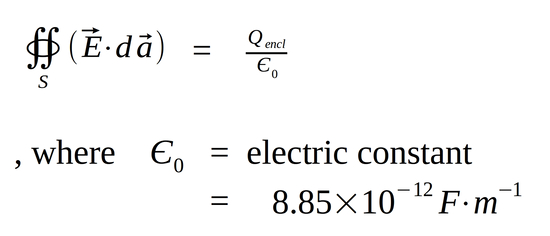
we use the divergence theorem to rewrite the left side of the equation as:

...which gives us:

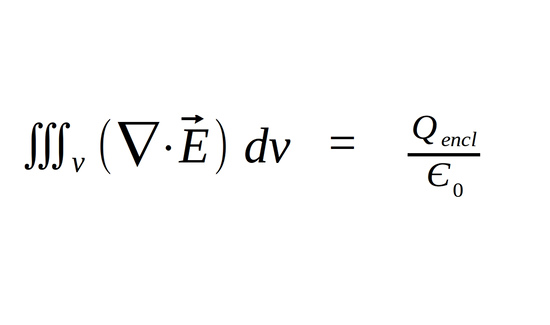
We now need to think about how we can rewrite the right-hand side of the equation in terms of a triple integral. When we think of the total charge enclosed by a Gaussian surface (Q encl), you may realize that this is essentially the same thing as integrating the volume charge density (rho) over the volume bounded by that Gaussian surface such that:

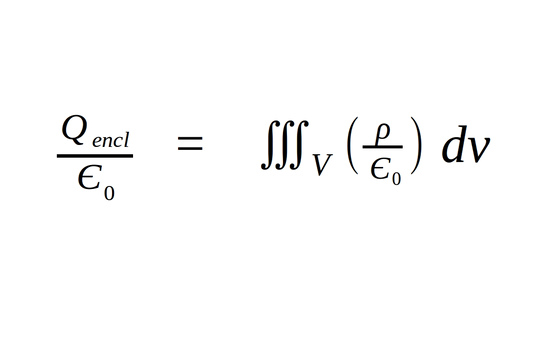
We now have:

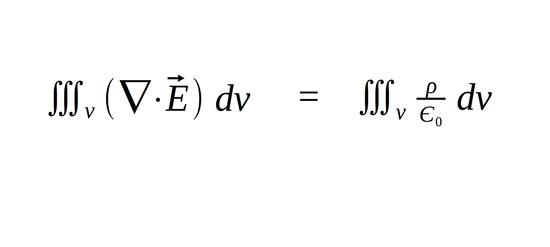
This is also sometimes referred to as Maxwell's 1st equation in "full integral form". Since the electric constant is exactly that (a constant), we can pull it outside of the integral leaving us with:

Maxwell's 1st Equation in full integral form:

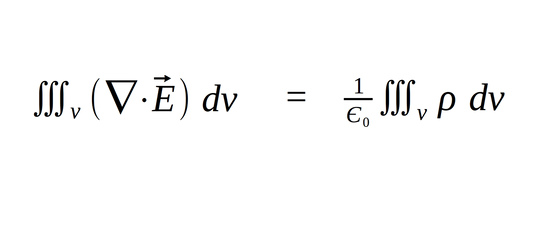
... and if two integrals are equal to each other, the terms being integrated are also equal such that we obtain:

Maxwell's 1st Equation in differential form:

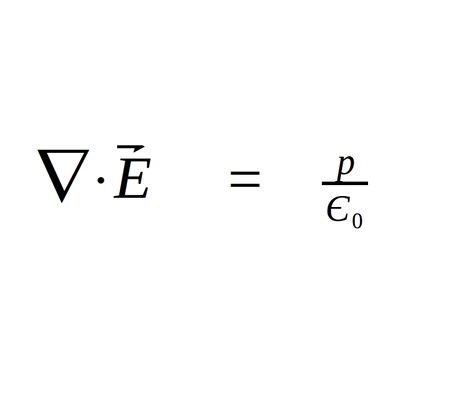
Maxwell's 2nd Equation (Gauss's Law for Magnetic Fields)

Beginning with:

... again use the Divergence Theorem to rewrite the left side of the equation as:

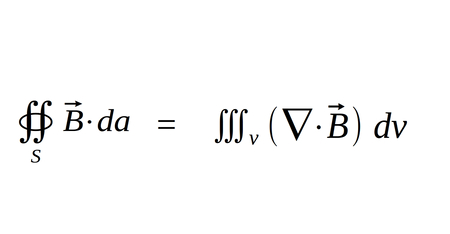
...which gives us:

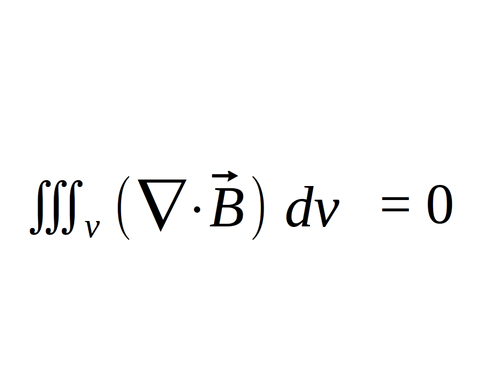
We also know that for an integral to equal zero, the term being integrated has to be zero. Therefore we now have:

Maxwell's 2nd Equation in differential form:

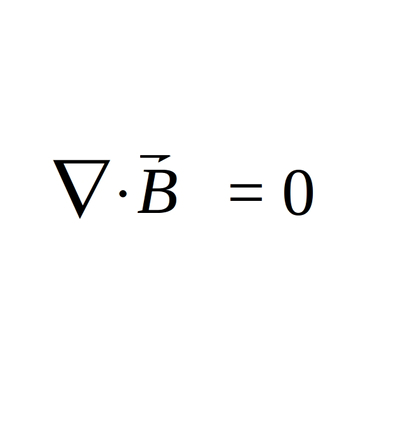
Maxwell's 3rd Equation (Ampere's Law, including displacement current)

Here we start with Maxwell's 3rd equation with the inclusion of displacement current:

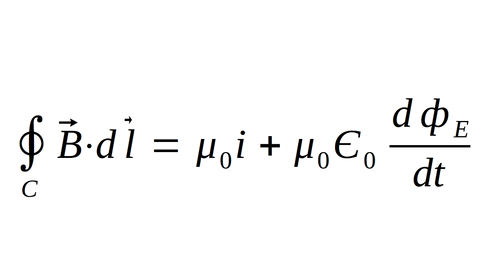
This time we will use Stokes' Theorem to rewrite the left hand side of the equation as:

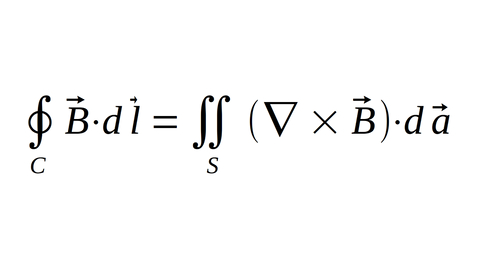
Now we have to come up with a way to represent the right-hand side of the equation as an integration over a two-dimensional area. The total current (i) can be thought of as current area density (J) integrated over an area. Also, by definition, electric flux is defined as:

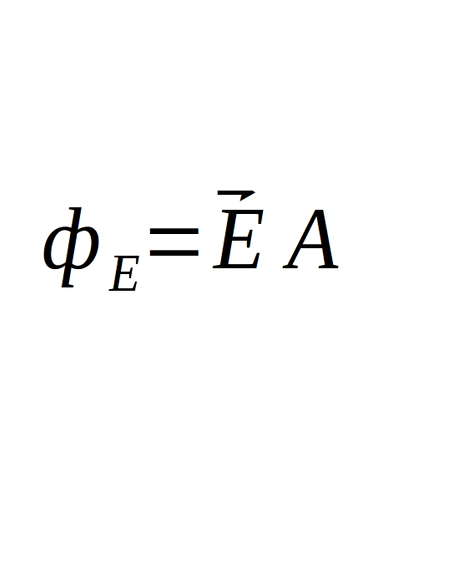
Therefore we can represent the total electric flux by integrating the electric field across the area of the Gaussian surface:

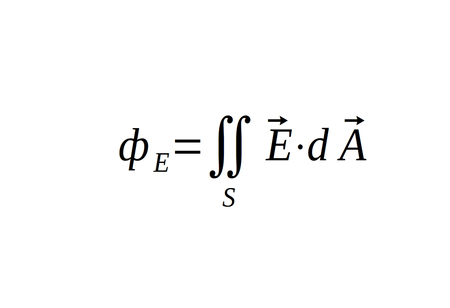
...and with these substitutions we get:

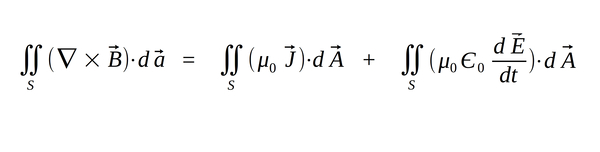
On the right-hand side of the equation, the two surface integrals can actually be combined into one surface integral over the same area. This means that the terms inside the integral on the left side equal the terms inside the integral on the right side and we have:

Maxwell's 3rd Equation in differential form:

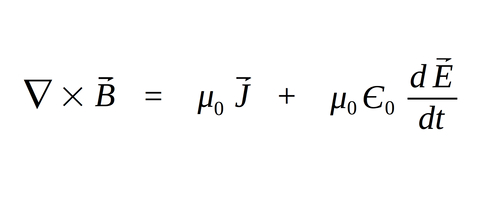
Maxwell's 4th Equation (Faraday's law of Induction)

For Maxwell's 4th (and final) equation we begin with:

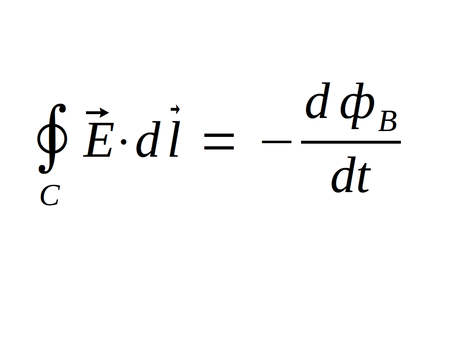
Stokes' Theorem is again used to rewrite the left side of the equation as:

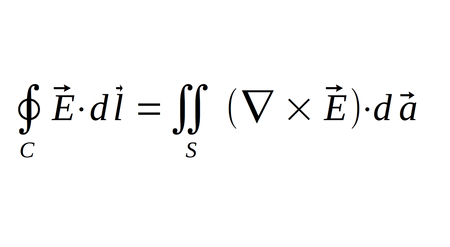
In order to convert the right side of the equation to a surface integral, recall the definition of magnetic flux:

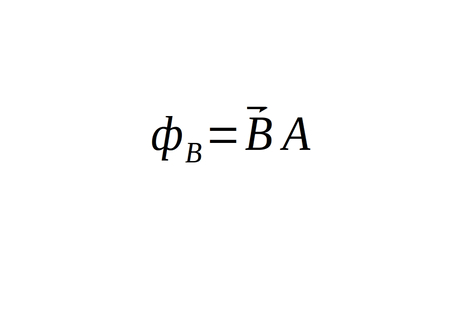
...and just as with electric flux, magnetic flux can be represented by integrating the magnetic field across the area of the Gaussian surface:

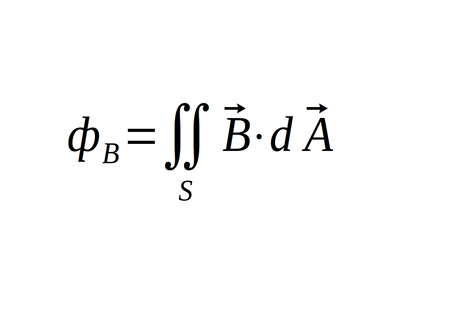
After making the substitutions we have:

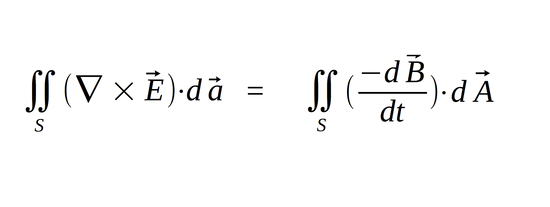
...and with the integral signs canceling we achieve:

Maxwell's 4th Equation in differential form: