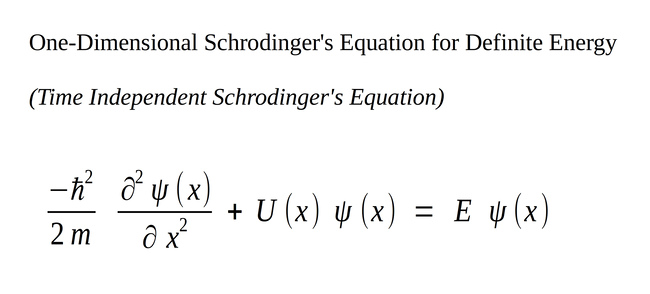One Dimensional Schrodinger's Equation for a Definite Energy (Stationary State)
Given the one-dimensional sinusoidal wave function for a particle:
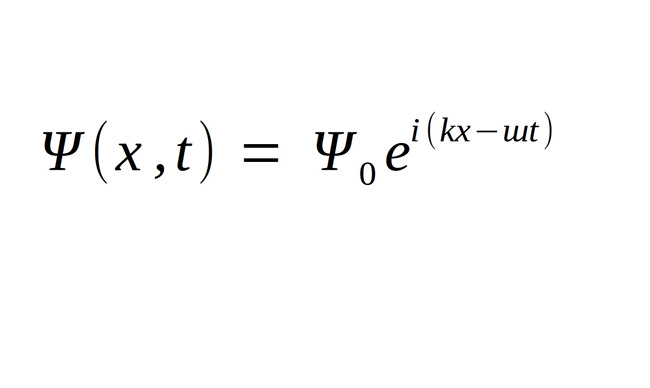
and the one-dimensional Schrodinger's equation (with potential energy):
(eqn I)
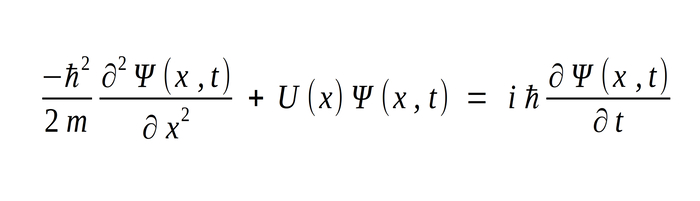
We can obtain a time independent Schrodinger's equation for definite energy (stationary state).
Separation Technique
We start by recognizing that the given particle wave function can be separated into two functions of both position and time:
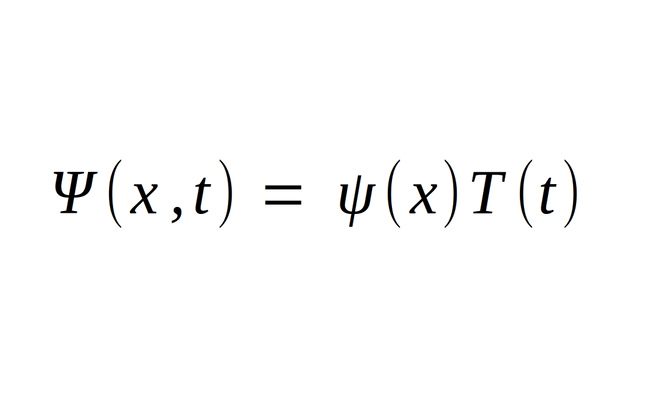
where lower-case psi(x) is the time independent wave function
By taking the derivative of the above (separated) function, with respect to x, we get:
(eqn II)
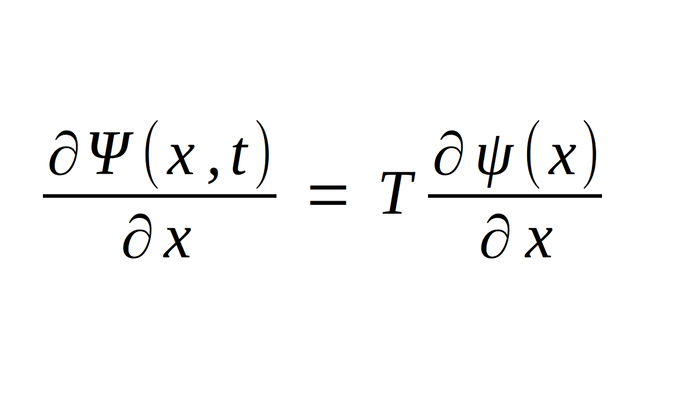
(note: T = T(t))
... and taking the second derivative with respect to x gives us:
(eqn III)
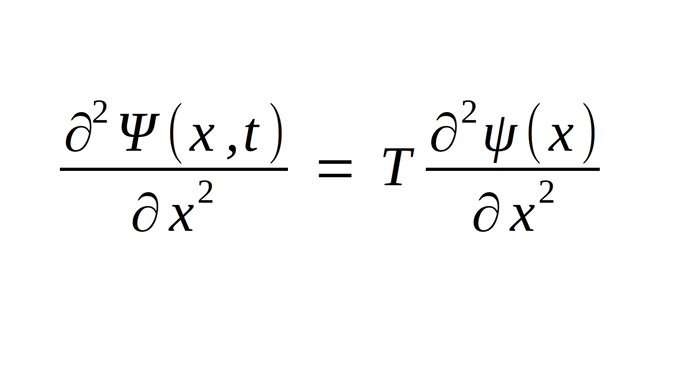
Lastly, taking the derivative of the separated wave function with respect to T gives us:
(eqn IV)
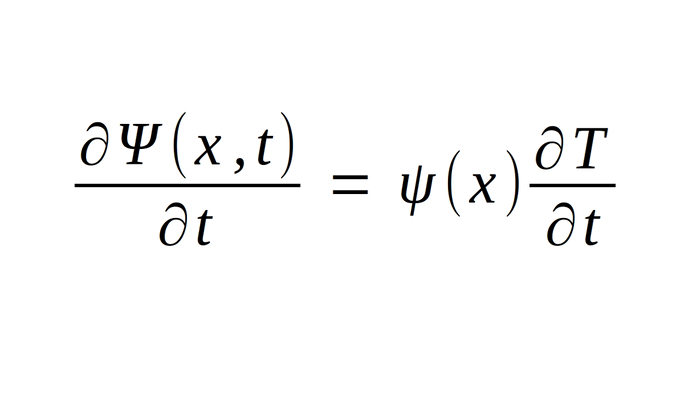
By substituting equations 2, 3, and 4 into equation #1 we obtain:
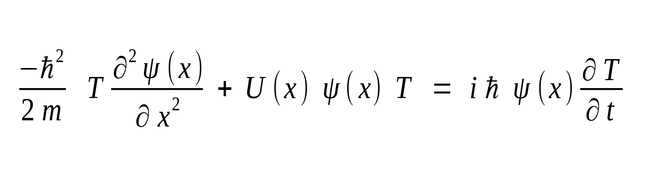
Dividing through by T (tau) results in the following:
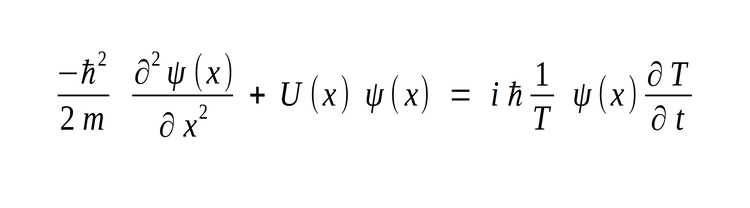
Now examine the right-hand side of the equation and recognize that the time function (T) and it's derivative are equal to the following:
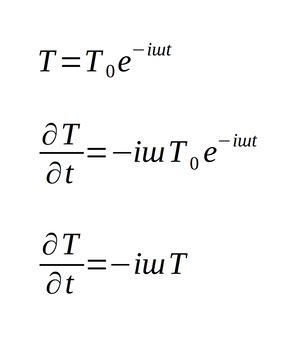
Therefore, if we substitute the above derivative of T into the right hand side of our equation, the imaginary part (i) becomes 1 and the T cancels leaving us with:
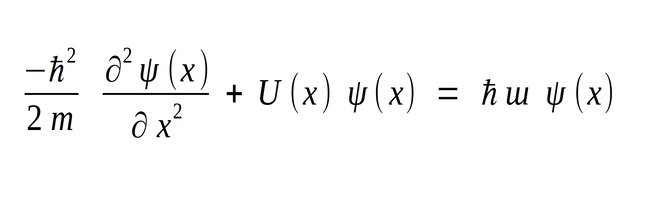
Also recall that:
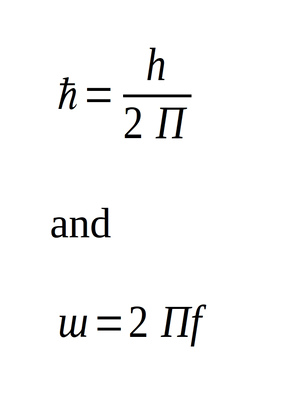
Which turns our equation into:
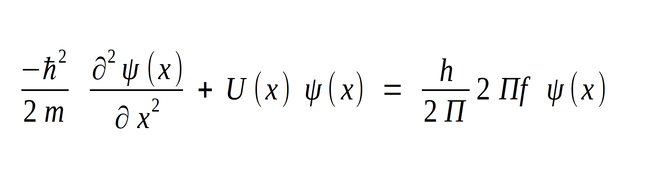
...which cancels the 2 pi terms:
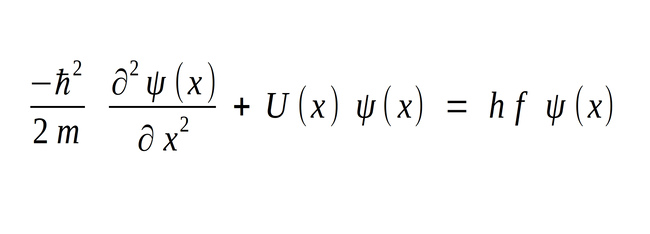
Also recall that:
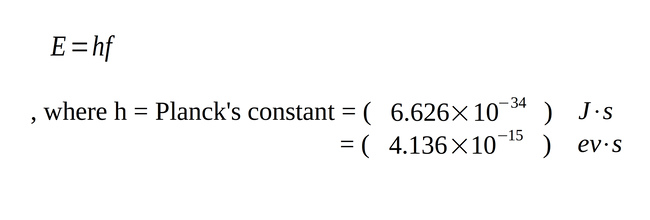
...and finally we arrive at: