Three-Phase Loads

In a three-phase system, loads can also be connected in a Wye or Delta fashion:

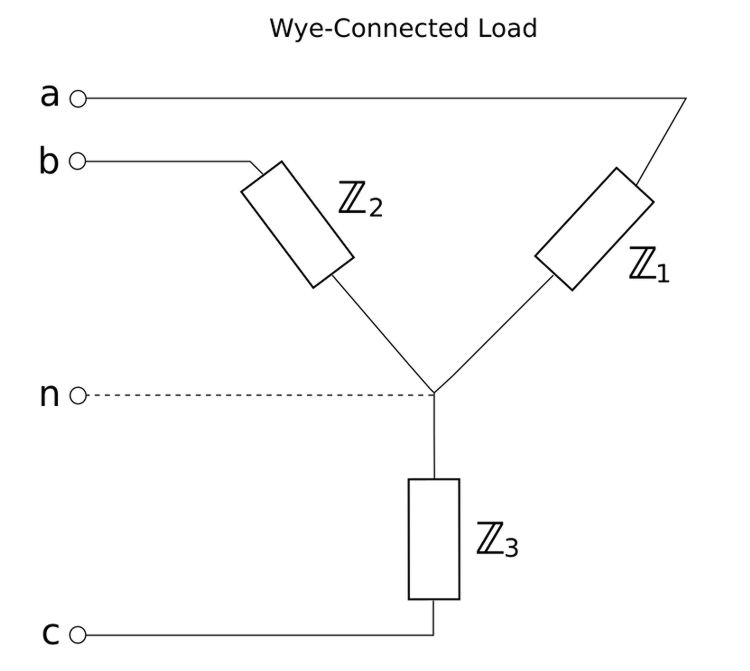
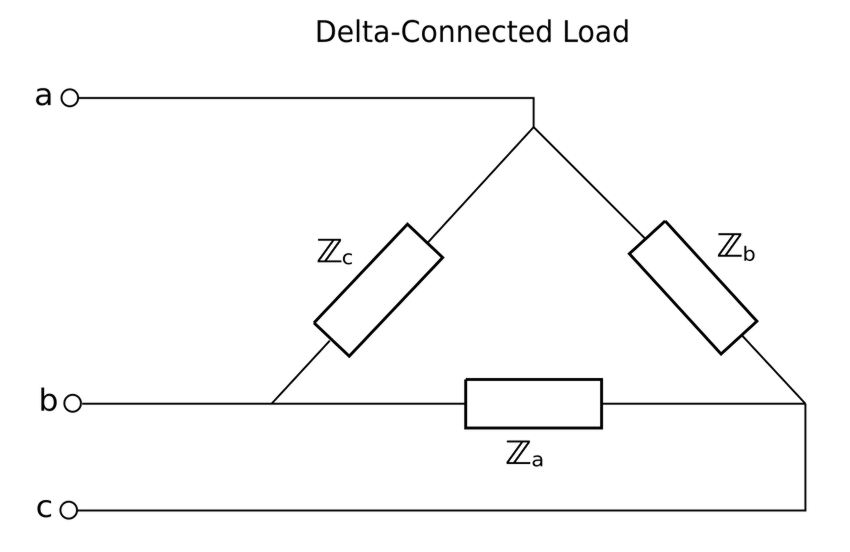
For a Y-connected load, the neutral line may or may not be present depending on whether the system is 3 or 4 wire. For a delta-connected load, a neutral connection is not possible.

Balanced Load:

In a three-phase system, a balanced load is one where the phase impedances are equal in magnitude and phase. First, lets look at how we go about a Wye to Delta or Delta to Y conversion for impedances. (It's the same process as for resistances.) Recall the familiar schematic shown below which depicts a wye circuit inside a delta circuit:

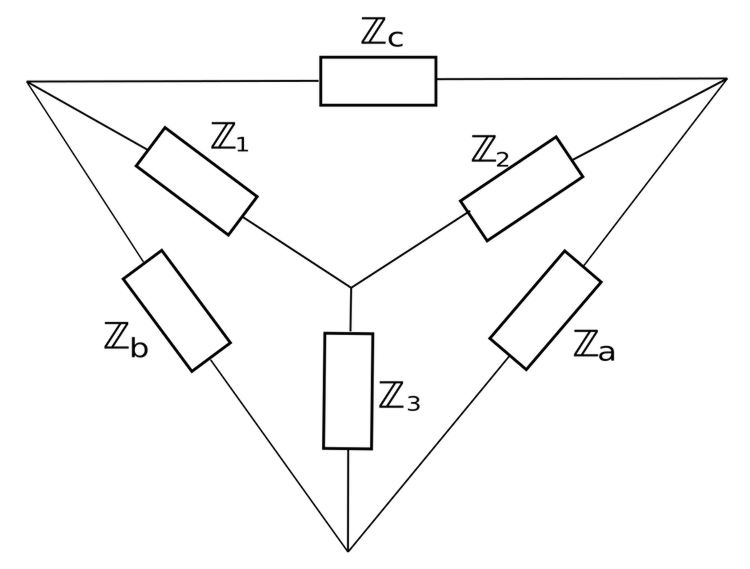
For a Y to Delta conversion we have:

$$ \mathbb{Z}_a = \frac{\mathbb{Z}_1 \mathbb{Z}_2 + \mathbb{Z}_2 \mathbb{Z}_3 + \mathbb{Z}_3 \mathbb{Z}_1}{\mathbb{Z}_1} $$ $$ \mathbb{Z}_b = \frac{\mathbb{Z}_1 \mathbb{Z}_2 + \mathbb{Z}_2 \mathbb{Z}_3 + \mathbb{Z}_3 \mathbb{Z}_1}{\mathbb{Z}_2} $$ $$ \mathbb{Z}_c = \frac{\mathbb{Z}_1 \mathbb{Z}_2 + \mathbb{Z}_2 \mathbb{Z}_3 + \mathbb{Z}_3 \mathbb{Z}_1}{\mathbb{Z}_3} $$

For a Delta to Wye conversion we have:

$$ \mathbb{Z}_1 = \frac{\mathbb{Z}_b \mathbb{Z}_c}{\mathbb{Z}_a + \mathbb{Z}_b + \mathbb{Z}_c} $$ $$ \mathbb{Z}_2 = \frac{\mathbb{Z}_c \mathbb{Z}_a}{\mathbb{Z}_a + \mathbb{Z}_b + \mathbb{Z}_c} $$ $$ \mathbb{Z}_3 = \frac{\mathbb{Z}_a \mathbb{Z}_b}{\mathbb{Z}_a + \mathbb{Z}_b + \mathbb{Z}_c} $$

When a Wye or Delta circuit is balanced we have: $$ \mathbb{Z}_Y = \mathbb{Z}_1 = \mathbb{Z}_2 = \mathbb{Z}_3 $$ $$ \mathbb{Z}_{\Delta} = \mathbb{Z}_a = \mathbb{Z}_b = \mathbb{Z}_c $$ Therefore, to convert a balanced three-phase Y circuit to a delta circuit we would get: $$ \mathbb{Z}_{\Delta} = \frac{\mathbb{Z}_Y \mathbb{Z}_Y + \mathbb{Z}_Y \mathbb{Z}_Y + \mathbb{Z}_Y \mathbb{Z}_Y}{\mathbb{Z}_Y} $$ $$ \mathbb{Z}_{\Delta} = \frac{3(\mathbb{Z}_Y)^2}{\mathbb{Z}_Y} $$

Wye to Delta conversion for a balanced load:

$$ \mathbb{Z}_{\Delta} = 3\mathbb{Z}_Y $$

Similarly, we can use simple algebra on the above expression OR plug Z_delta into the formulas for a Delta to Wye conversion in order to get the following:

Delta to Wye conversion for a balanced load:

$$ \mathbb{Z}_Y = \frac{1}{3}\mathbb{Z}_{\Delta} $$

Now that we have introduced three-phase sources and three-phase loads, you may realize that we can have four possible connection scenarios in regards to the source and the load:

1. $$ Y-Y $$
2. $$ \Delta - Y $$
3. $$ \Delta - \Delta $$
4. $$ \Delta - Y $$

In the next section we will take a look at Balanced Wye-Wye connections.

Continue on to Balanced Wye-Wye Systems...