This next type of three-phase connection consists of a balanced 3-phase source that powers a balanced delta-connected load. In this situation, a neutral connection between source and load is not possible (as shown below:)
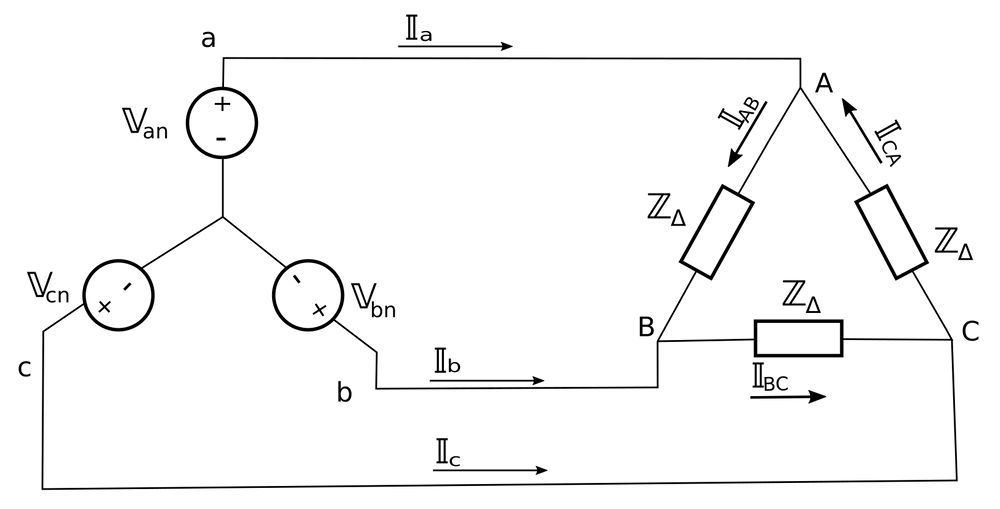
In the previous sections, we determined that the phase voltages for a balanced Y-connected source with a postive ("abc") sequence are: $$ \mathbb{V}_{an} = V_p \angle 0^{\circ} $$ $$ \mathbb{V}_{bn} = V_p \angle (-120^{\circ}) $$ $$ \mathbb{V}_{cn} = V_p \angle 120^{\circ} $$ ...and the line voltages are: $$ \mathbb{V}_{ab} = \sqrt{3} \; V_p \angle 30^{\circ} $$ $$ \mathbb{V}_{bc} = \sqrt{3} \; V_p \angle (-90^{\circ}) $$ $$ \mathbb{V}_{ca} = \sqrt{3} \; V_p \angle 150^{\circ} $$ Notice that the line voltages are equal to the voltages across the load impedances: $$ \mathbb{V}_{ab} = \mathbb{V}_{AB} \;,\;\;\; \mathbb{V}_{bc} = \mathbb{V}_{BC} \;,\;\;\; \mathbb{V}_{ca} = \mathbb{V}_{CA} $$
Phase currents:
Applying Ohm's Law will give us the following expressions for the current through the load impedances: $$ \mathbb{I}_{AB} = \frac{\mathbb{V}_{AB}}{\mathbb{Z}_{\Delta}} \;,\;\;\; \mathbb{I}_{BC} = \frac{\mathbb{V}_{BC}}{\mathbb{Z}_{\Delta}} \;,\;\;\; \mathbb{I}_{CA} = \frac{\mathbb{V}_{CA}}{\mathbb{Z}_{\Delta}}$$ We would also get the same expressions if we were to use Kirchhoff's Voltage Law (KVL) around the loops created by the phases. For example, if we apply KCL around the loop aABbna (where "n" is the neutral point of the Y-connected source) we would get: $$ -\mathbb{V}_{an} + \mathbb{I}_{AB} \mathbb{Z}_{\Delta} + \mathbb{V}_{bn} = 0 $$ $$ \mathbb{I}_{AB} = \frac{\mathbb{V}_{an} - \mathbb{V}_{bn}}{\mathbb{Z}_{\Delta}} $$ $$ \qquad = \frac{\mathbb{V}_{AB}}{\mathbb{Z}_{\Delta}} $$ In a balanced Y-Delta connection, the currents through the load impedances are equal in magnitude but out of phase with each other by 120 degrees.
Line Currents:
If we were to apply Kirchhoff's Current Law (KCL) at node "A", we would get: $$ \mathbb{I}_a + \mathbb{I}_{CA} = \mathbb{I}_{AB} $$ $$ \mathbb{I}_a = \mathbb{I}_{AB} - \mathbb{I}_{CA} $$
We know that: $$ \mathbb{I}_{CA} = \mathbb{I}_{AB} \angle (-240^{\circ}) $$ ...therefore:
$$ \mathbb{I}_a = \mathbb{I}_{AB} - \mathbb{I}_{AB} \angle (-240^{\circ}) $$ $$ \qquad = \mathbb{I}_{AB} (1-1 \angle (-240^{\circ}) ) $$ $$ \qquad = \mathbb{I}_{AB} [1-(-0.5+j\frac{\sqrt{3}}{2})] $$ $$ \qquad = \mathbb{I}_{AB} (\frac{3}{2} - j\frac{\sqrt{3}}{2}) $$ $$ \mathbb{I}_a = \sqrt{3}\mathbb{I}_{AB} \angle 30^{\circ} $$ We see that the magnitude of the line current is sqrt(3) times the magnitude of the phase current. The line current is also shown to lag the corresponding phase current by 30 degrees (For a positive sequence). We would come to a similar conclusion if we were to apply KCL at the other two nodes in the delta-connected source. In general we can say that:
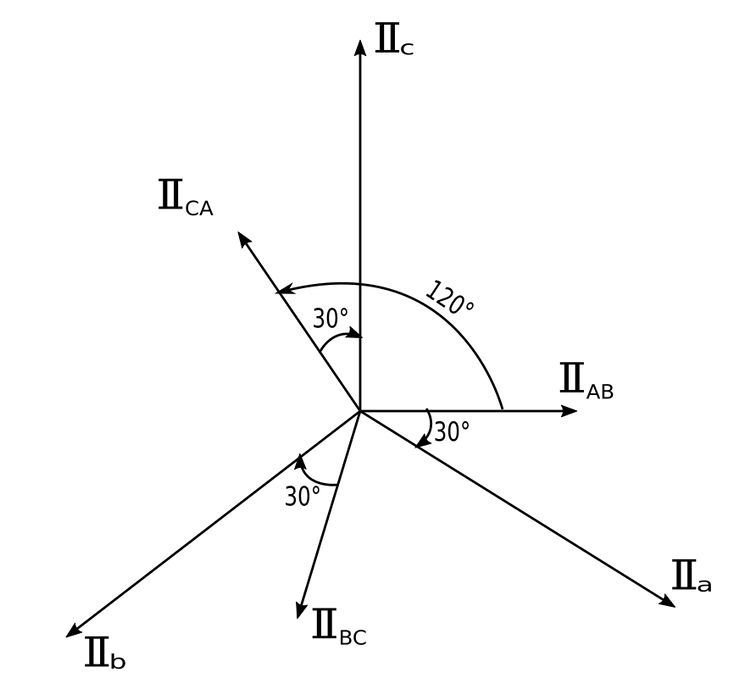
The following phase diagram shows the realtionships between line and phase currents:
Alternative method of analysis (Transformations):
We can also transform the delta-connected load to a Y-connected load. In the section regarding balanced 3-phase loads, we learned that when performing a Delta to Wye transformation, the impedance value for the newly formed Y-connected load is: $$ \mathbb{Z}_Y = \frac{1}{3}\mathbb{Z}_{\Delta} $$ The line currents can then be calculated on a per-phase basis. For example, for phase "a":
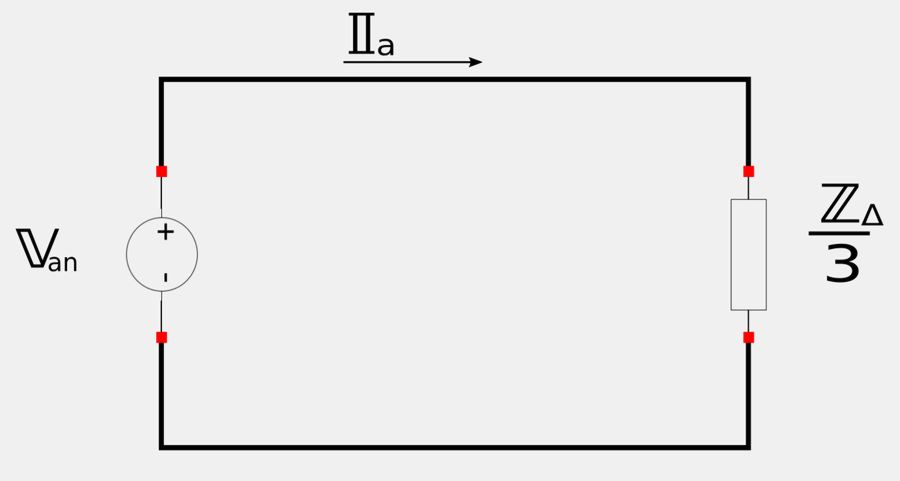
For the phase currents we would use equation #2 to calculate the magnitude: $$ I_p = \frac{I_l}{\sqrt{3}} $$ The angle of the phase current would be determined through our knowledge that phase currents lead line currents by 30 degrees.
In the next page we will look at an example problem involving a Y-Delta circuit.
Continue on to Y-Delta example problem...
