A Balanced Wye-Wye connection is a three-phase system with a balanced Y-connected source and a balanced Y-connected load. Later on we will learn that any balanced three-phase system can be reduced to an equivalent Y-Y system. For this reason, understanding the Y-Y system is important to being able to solve all balanced three-phase systems. Our Y-Y connection is shown below:
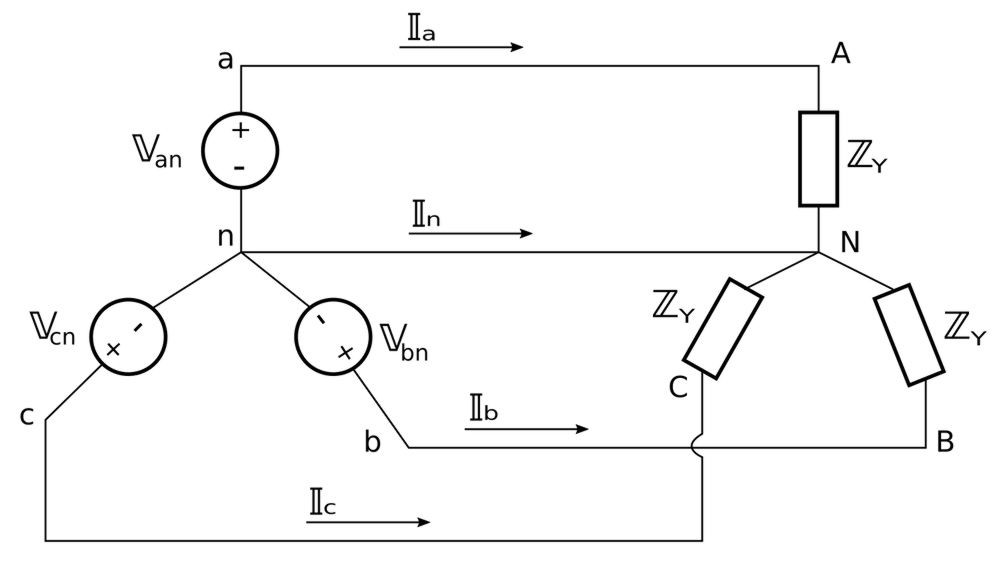
Phase Voltages:
Assuming an "abc" (positive) sequence we have the following: $$ \mathbb{V}_{an} = V_p \angle 0^{\circ} $$ $$ \mathbb{V}_{bn} = V_p \angle (-120^{\circ})$$ $$ \mathbb{V}_{cn} = V_p \angle 120^{\circ} $$ The three expressions above are known as "phase voltages" Phase voltages are the voltage across any single component.
Line Voltages:
A couple of sections back we learned that a line voltage is the voltage between two conductors. Line voltages can also be expressed in terms of phase voltages (and vice-versa.) Consider the line voltage between "a" and "b" in our circuit above: $$ \mathbb{V}_{ab} = \mathbb{V}_{an} + \mathbb{V}_{nb} $$ $$ \;\;\;\;\; = \mathbb{V}_{an} - \mathbb{V}_{bn} $$ $$ \;\;\;\;\; = V_p \angle 0^{\circ} - V_p \angle (-120^{\circ}) $$ $$ \;\;\;\;\; = V_p\Big[1\angle 0^{\circ} - 1 \angle (-120^{\circ})\Big] $$ $$ \;\;\;\;\; = V_p \Big[ 1 + \frac{1}{2} + j\frac{\sqrt{3}}{2} \Big] $$ $$ \;\;\;\;\; = V_p \Big[ \frac{3}{2} + j\frac{\sqrt{3}}{2} \Big] $$ $$ \mathbb{V}_{ab} = \sqrt{3} \; V_p \angle 30^{\circ} $$ In a similar manner, we can get the following expressions for the remaining line voltages: $$ \mathbb{V}_{bc} = \mathbb{V}_{bn} + \mathbb{V}_{nc} $$ $$ \;\;\;\;\; = \mathbb{V}_{bn} - \mathbb{V}_{cn} $$ $$ \mathbb{V}_{bc} = \sqrt{3} \; V_p \angle (-90^{\circ}) $$
$$ \mathbb{V}_{ca} = \mathbb{V}_{cn} + \mathbb{V}_{na} $$ $$ \;\;\;\;\; = \mathbb{V}_{cn} - \mathbb{V}_{an} $$ $$ \mathbb{V}_{ca} = \sqrt{3} \; V_p \angle (-210^{\circ}) $$
At this point we realize that the magnitude of the line voltage can be expressed as the following:
Magnitude of line voltage in terms of phase voltage (and vice-versa):
$$ V_L = \sqrt{3} \; V_p \qquad and \qquad V_p = \frac{1}{\sqrt{3}} V_L $$ ...where: $$ V_p = |\mathbb{V}_{an}| = |\mathbb{V}_{bn}| = |\mathbb{V}_{cn}| $$ and $$ V_L = |\mathbb{V}_{ab}| = |\mathbb{V}_{bc}| = |\mathbb{V}_{ca}| $$
Also, notice that the line voltages lead their corresponding phase voltages by 30 degrees: $$ \mathbb{V}_{ab} = \sqrt{3} \; V_p \angle 30^{\circ} \qquad, \; \; \; \; \; \mathbb{V}_{an} = V_p \angle 0^{\circ} $$ $$ \mathbb{V}_{bc} = \sqrt{3} \; V_p \angle (-90^{\circ}) \qquad , \; \mathbb{V}_{bn} = V_p \angle (-120^{\circ}) $$
$$ \mathbb{V}_{ca} = \sqrt{3} \; V_p \angle (-210^{\circ}) = \sqrt{3} \; V_p \angle 150^{\circ} \qquad, \mathbb{V}_{cn} = V_p \angle(-240^{\circ}) = V_p \angle (120^{\circ}) $$
The relationship between line and phase voltage can also be shown by means of the following vector diagram showing the vector addition via the parallelogram technique. For example, consider phase "a" shown below:
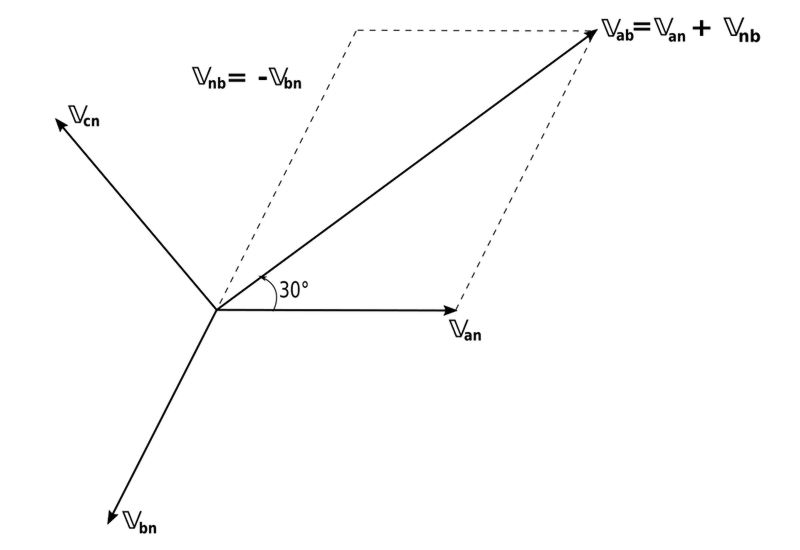
Below we see the phase diagram showing the remaining phases:
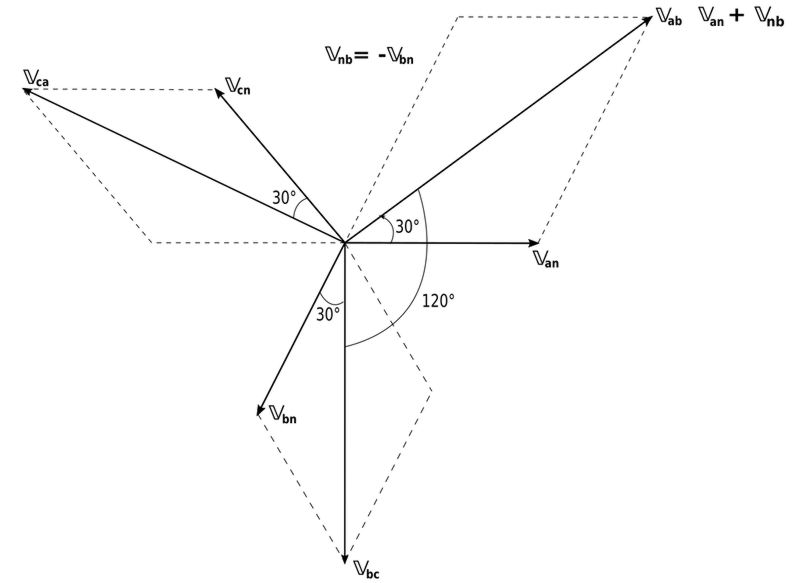
Regarding the line voltages, we see above that V_ab leads V_bc by 120 degrees and that V_bc leads V_ca by 120 degrees. You will also find that the line voltages sum to zero (as do the phase voltages.)
Determining Line Current from Phase Voltages and Phase Impedances:
Recall our Y-Y system with a "positive" sequence:

Starting with phase "a", if we apply Kirchhoff's Voltage Law (KVL) to each phase we would get: $$ \mathbb{I}_a = \frac{\mathbb{V}_{an}}{\mathbb{Z}_Y} = \frac{V_a \angle 0^{\circ}}{\mathbb{Z}_Y}$$ For phase "b": $$ \mathbb{I}_b = \frac{\mathbb{V}_{bn}}{\mathbb{Z}_Y} $$ However, recall that for a balanced system the magnitudes of the phase voltages are equal, and as such the magnitude of the phase voltage for "b" is the same as "a" but lags by 120 degrees. Therefore: $$ \mathbb{I}_b = \frac{\mathbb{V}_{bn}}{\mathbb{Z}_Y} = \frac{V_a \angle (-120^{\circ})}{\mathbb{Z}_Y} $$ $$ \qquad = \Big( \frac{V_a}{\mathbb{Z}_Y} \Big) \Big(1\angle (-120^{\circ})\Big) $$ $$ \mathbb{I}_b = \mathbb{I}_a \angle (-120^{\circ}) $$ Similarly, for phase "c" we have: $$ \mathbb{I}_c = \frac{\mathbb{V}_{cn}}{\mathbb{Z}_Y} $$ Once again, we know that the magnitude of the phase voltages are equal and that the magnitude of the phase voltage for "c" is the same as "a" but lags "a" by 240 degrees: $$ \mathbb{I}_c = \frac{\mathbb{V}_{cn}}{\mathbb{Z}_Y} = \frac{V_a \angle (-240^{\circ})}{\mathbb{Z}_Y} $$ $$ \qquad = \Big( \frac{V_a}{\mathbb{Z}_Y} \Big) \Big(1\angle (-240^{\circ})\Big) $$ $$ \mathbb{I}_c = \mathbb{I}_a \angle (-240^{\circ}) $$
Expressions for Line Currents in a Balanced Y-Y System:
$$ \mathbb{I}_a = \frac{\mathbb{V}_{an}}{\mathbb{Z}_Y} = \frac{V_a \angle 0^{\circ}}{\mathbb{Z}_Y} $$ $$ \mathbb{I}_b = \mathbb{I}_a \angle (-120^{\circ}) $$ $$ \mathbb{I}_c = \mathbb{I}_a \angle (-240^{\circ}) = \mathbb{I}_a \angle 120^{\circ} $$
Just as with the phase voltages in a balanced Y-Y system, the line currents are also equal in magnitude and 120 degrees out of phase with each other. If you were to add the line currents together, you would also find that they also sum to zero: $$ \mathbb{I}_a + \mathbb{I}_b + \mathbb{I}_c = 0 $$
Neutral line current:
Additionally, note that the neutral line current can be expressed as: $$ \mathbb{I}_n = -(\mathbb{I}_a + \mathbb{I}_b + \mathbb{I}_c) $$ ...which means that: $$ \mathbb{I}_n = 0 $$ If the neutral line current is zero then the voltage across the neutral line is: $$ V_{nN} = \mathbb{Z}_n \mathbb{I}_n = 0 $$ We see that the voltage across the neutral line is zero. This essentially means that the neutral line can be removed without affecting the rest of the system.
Phase Current:
Phase Current is the current in each phase of the source or load. In a Wye-Wye system, phase current and line current are equal.
"Per-phase" Analysis:
When analyzing a balanced Y-Y system, it can be helpful to take a single phase and analyze it alone. For example we have phase "a" below:
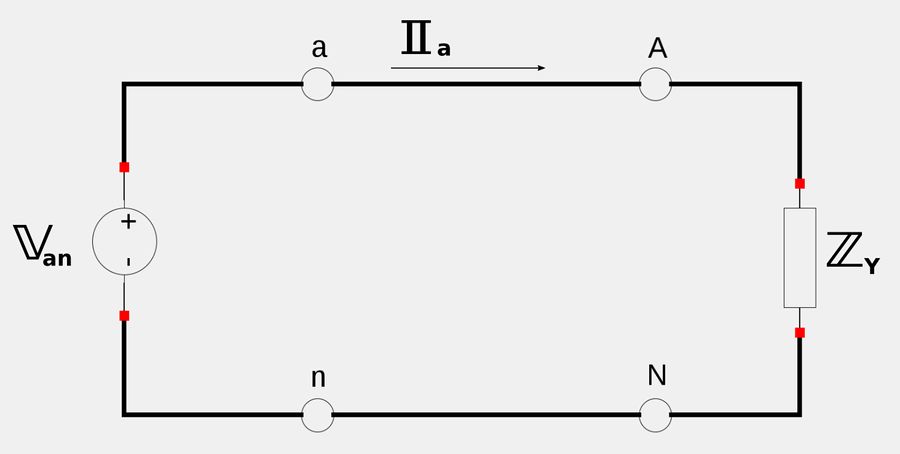
Once we determine the following: $$ \mathbb{I}_a = \frac{\mathbb{V}_{an}}{\mathbb{Z}_Y} $$ ...we can use the phase sequence to determine values for subsequent phases.
In the following page we will take a look at an example problem involving a balanced Wye-Wye system.
Continue on to Balanced Wye-Wye Systems (example problem)
