For the balanced Y-Y system shown below, determine the line currents and neutral current.
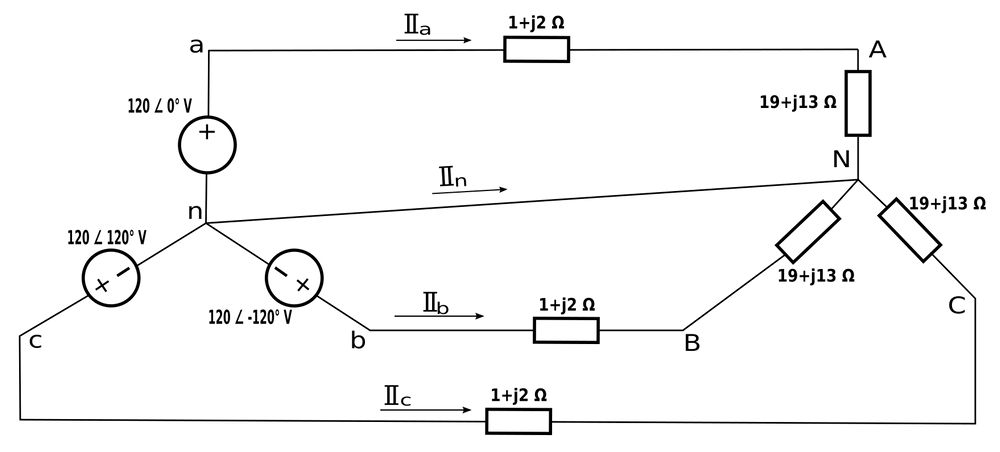
Furthermore, we are given the following load imedances (Z_L) and line imepdances (Z_l): $$ \mathbb{Z}_L = 19+j13 \; \Omega $$ $$ \mathbb{Z}_l = 1+j2 \; \Omega $$
Start by determining the line current for phase "a":
$$ \mathbb{I}_a = \frac{\mathbb{V}_{an}}{\mathbb{Z}_L + \mathbb{Z}_l} $$
Go ahead and calculate the series impedance combination for the load and line impedances: $$ \mathbb{Z}_L + \mathbb{Z}_l = (19+j13) + (1+j2) $$ $$ \qquad \;\;\; = 20+j15 \; \Omega $$ $$ \qquad \;\;\; = 25 \angle 36.87^{\circ} $$
$$ \mathbb{I}_a = \frac{120}{25 \angle 36.87^{\circ}} $$ $$ \mathbb{I}_a = 4.8 \angle (-36.87^{\circ}) \; A$$
Determine the line current for phase "b":
Knowing that this is a balanced Y-Y system with a "positive" (abc) sequence, we can quickly determine the line current for phase "b" as being equal in magnitude to phase "a" but lagging phase "a" by 120 degrees. Therefore: $$ \mathbb{I}_b = \mathbb{I}_a \angle (-120^{\circ}) $$ $$ \qquad = \Big[ 4.8 \angle (-36.87^{\circ}) \Big] \Big[ 1\angle (-120^{\circ}) \Big] $$ $$ \mathbb{I}_b = 4.8 \angle (-156.9^{\circ}) \; A$$
Determine the line current for phase "c":
Additionally (for the same reasons) we know that the line current for phase "c" is equal in magnitude to "a" and "b" but lags phase "b" by 120 degrees and lags phase "a" by 240 degrees. Therefore: $$ \mathbb{I}_c = \mathbb{I}_a \angle (-240^{\circ}) $$ $$ \qquad = \Big[ 4.8 \angle (-36.87^{\circ}) \Big] \Big[ 1\angle (-240^{\circ}) \Big] $$ $$ \mathbb{I}_c = 4.8 \angle (-276.9^{\circ}) \; A= 4.8 \angle 83.1^{\circ} \; A$$
Determine the neutral line current.
In the last section we learned that the neutral line current for a Y-Y system is zero. We can also prove it here through the following: $$ \mathbb{I}_a + \mathbb{I}_b + \mathbb{I}_c = 4.8 \angle (-36.87^{\circ}) + 4.8 \angle (-156.9^{\circ}) + 4.8 \angle 83.1^{\circ} $$ $$ = 4.8 [(3.84-j2.88)+(-4.415-j1.883)+(0.5767+j4.765)] $$ Due to rounding errors here, the value inside the brackets is close to zero, but would equal zero otherwise. $$ = 4.8(0) $$ $$ \mathbb{I}_a + \mathbb{I}_b + \mathbb{I}_c =0 $$ From the last page we know that: $$ \mathbb{I}_n = -(\mathbb{I}_a + \mathbb{I}_b + \mathbb{I}_c) $$ $$ \mathbb{I}_n = 0 \; A$$
Final Answer:
$$ \mathbb{I}_a = 4.8 \angle (-36.9^{\circ}) \; A$$ $$ \mathbb{I}_b = 4.8 \angle (-157^{\circ}) \; A$$ $$ \mathbb{I}_c = 4.8 \angle 83.1^{\circ} \; A$$ $$ \mathbb{I}_n = 0 \; A$$
Continue on to Balanced Wye-Delta Systems...
