We now take a look at a circuit where the source and load are both balanced and delta-connected:
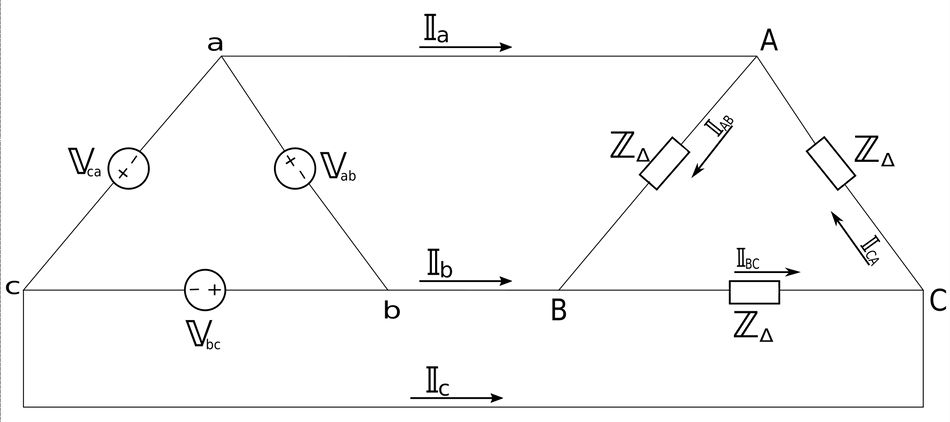
Once again, our goal here is to be able to determine the phase and line currents. Assuming a positive ("abc") sequence, the phase voltages of the source are: $$ \mathbb{V}_{ab} = V_p \angle 0^{\circ} $$ $$ \mathbb{V}_{bc} = V_p \angle (-120^{\circ}) $$ $$ \mathbb{V}_{ca} = V_p \angle 120^{\circ} $$ Also notice that for a delta-connected source, line voltage is the same as phase voltage. Additionally, assuming there is no line impedance the phase voltage of the delta-connected source is equal to the voltage across the load impedance: $$ \mathbb{V}_{ab} = \mathbb{V}_{AB} \qquad,\mathbb{V}_{bc} = \mathbb{V}_{BC} \qquad, \mathbb{V}_{ca} = \mathbb{V}_{CA} $$
Phase Currents:
The phase currents can now be determined by using Ohm's Law: $$ \mathbb{I}_{AB} = \frac{\mathbb{V}_{AB}}{\mathbb{Z}_{\Delta}} = \frac{\mathbb{V}_{ab}}{\mathbb{Z}_{\Delta}} $$ $$ \mathbb{I}_{BC} = \frac{\mathbb{V}_{BC}}{\mathbb{Z}_{\Delta}} = \frac{\mathbb{V}_{bc}}{\mathbb{Z}_{\Delta}} $$ $$ \mathbb{I}_{CA} = \frac{\mathbb{V}_{CA}}{\mathbb{Z}_{\Delta}} = \frac{\mathbb{V}_{ca}}{\mathbb{Z}_{\Delta}} $$
Line Currents:
By applying Kirchhoff's Current Law (KCL) at node A, B and C we get: $$ \mathbb{I}_a = \mathbb{I}_{AB} - \mathbb{I}_{CA} $$ $$ \mathbb{I}_b = \mathbb{I}_{BC} - \mathbb{I}_{AB} $$ $$ \mathbb{I}_c = \mathbb{I}_{CA} - \mathbb{I}_{BC} $$ Just as with Y-delta connections, each line current lags its corresponding phase current by 30 degrees. Additionally, the magnitude of the line current is sqrt(3) times the magnitude of the phase current.
$$ I_L = \sqrt{3} \; I_p $$ ...where: $$ I_L = magnitude \; of \; line \; current. $$ $$ I_p = magnitude \; of \; phase \; current. $$ Line current leads phase current by 30 degrees. $$ \mathbb{I}_a = \sqrt{3} \; \mathbb{I}_{AB} \angle (-30^{\circ}) $$ $$ \mathbb{I}_b = \sqrt{3} \; \mathbb{I}_{BC} \angle (-30^{\circ}) $$ $$ \mathbb{I}_c = \sqrt{3} \; \mathbb{I}_{CA} \angle (-30^{\circ}) $$
Analysis by transformation:
Just as we did with three-phase Y-Delta circuits, we can convert the delta-connected source and load to their Y-equivalent circuits to make the analysis more convenient. The impedance conversion is as follows: $$ \mathbb{Z}_Y = \frac{1}{3} \mathbb{Z}_{\Delta} $$
In the next page we will look at an example problem involving a Delta-Delta circuit.
Continue on to Y-Delta example problem...
