Determine the the line current (Ia) and phase current (I_BC) of the following circuit:
Take as given the following load impedance value: $$ \mathbb{Z}_L = 8.66+j5 = 10 \angle 30^{\circ} $$ (Additionally, determine the power factor of the load.)
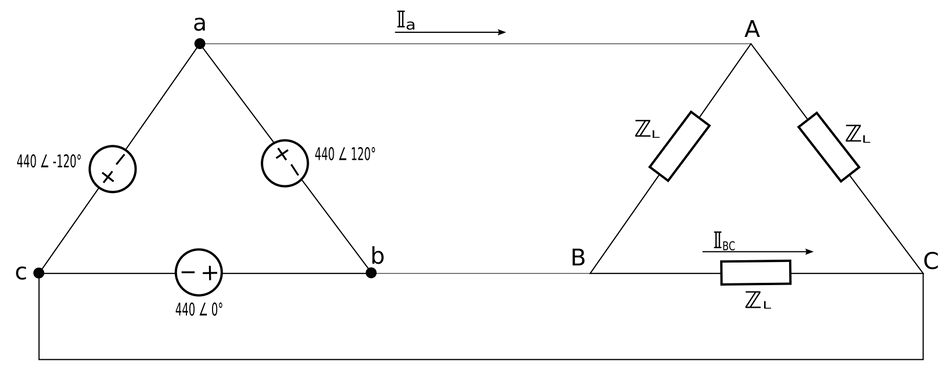
Phase Current
We start by determining the phase current. $$ \mathbb{I}_p = \frac{\mathbb{V}_p}{\mathbb{Z}_{\Delta}} $$ $$ \mathbb{I}_{BC} = \frac{\mathbb{V}_{BC}}{\mathbb{Z}_L} $$ $$ \mathbb{I}_{BC} = \frac{440 \angle 0^{\circ}}{10 \angle 30^{\circ}} $$
$$ \mathbb{I}_{BC} = 44 \angle (-30^{\circ}) $$
Line Current
In the previous section we learned that line currents lag phase currents by 30 degrees in a balanced delta-delta connected system and that line currents can be expressed in terms of phase currents as follows: $$\mathbb{I}_L = \sqrt{3} \; \mathbb{I}_p \angle (-30^{\circ}) $$ In order to determine the line current I_a, we first need to determine its corresponding phase current I_AB. $$ \mathbb{I}_{AB} = \frac{\mathbb{V}_{AB}}{\mathbb{Z}_L} = \frac{440 \angle 120^{\circ}}{10 \angle 30^{\circ}} $$ $$ \mathbb{I}_{AB} = 44 \angle 90^{\circ} $$ We can now determine the line current: $$ \mathbb{I}_a = \sqrt{3} \; \mathbb{I}_{AB} \angle (-30^{\circ}) $$ $$ \;\;= \Big[ \sqrt{3} \; \angle (-30^{\circ}) \Big] \Big[ 44 \angle 90^{\circ} \Big] $$
$$ \mathbb{I}_a = 76.21 \angle 60^{\circ} $$
Calculate the power factor of the load:
We start by determining the complex power expression for a single phase of the load: $$ \mathbb{S} = I_{rms}^2 \mathbb{Z} $$ Up above, we have already determine the phase current for phase "BC". Since this is a balanced system, the magnitude of the current through each phase is the same. Therefore we plug the magnitude of the phase current for phase "BC" (44) into the above expression. Additionally, the load impedance is the same for each phase. Therefore: $$ \mathbb{S}_{BC} = \mathbb{S}_{phase} = (44^2) (10 \angle 30^{\circ}) $$ $$ \mathbb{S}_{phase} = (19360 \angle 30^{\circ}) \qquad, (Eqn \; 1)$$ In our discussion on complex power, we learned that one of the four expressions for complex power is: $$ \mathbb{S} = V_{rms} \; I_{rms} \angle (\theta_v-\theta_i) \qquad, (Eqn \; 2) $$ ...where:: $$ \theta_v-\theta_i = power \; factor \; angle$$ If we compare equations 1 and 2 we realize that the power factor angle for our example circuit is: $$ \theta_p = 30^{\circ} $$ Remember, since this is a balanced system, the power factor angle is the same for all three phases.
Recall the definition of power factor: $$ P_f = \cos(\theta_p) $$ So, the power factor for a single phase of our circuit is: $$ P_f = \cos(30^{\circ}) $$ ...and again, since this is a balanced system, each phase has the same power factor which means the entire balanced load has a power factor of:
$$ P_f = 0.866 $$
Continue on to Balanced Delta-Wye Systems...
