A balanced Delta-Wye connection consists of a balanced delta-connected source driving a balanced Y-connected load as seen below:
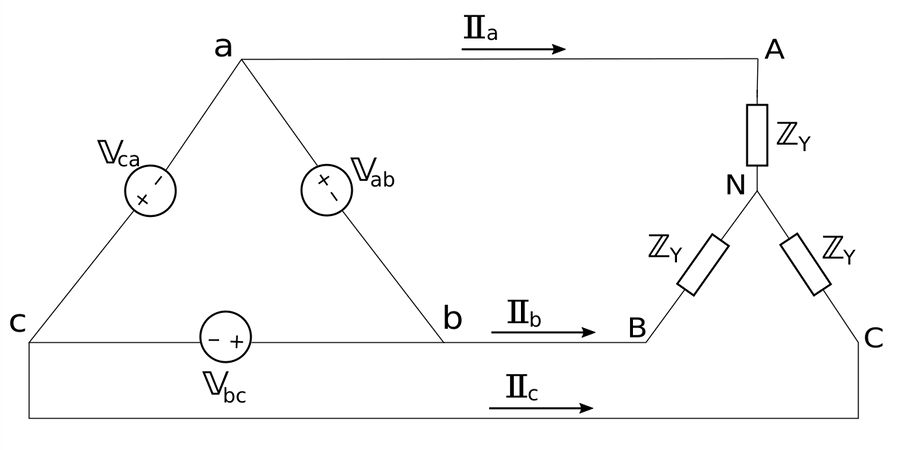
Assuming a positive ("abc") sequence, our phase voltages are as follows: $$ \mathbb{V}_{ab} = V_p \angle 0^{\circ} $$ $$ \mathbb{V}_{bc} = V_p \angle (-120^{\circ}) $$ $$ \mathbb{V}_{ca} = V_p \angle 120^{\circ} $$ Also, notice that the phase voltages are equal to the line voltages.
Determining line currents:
If we were to apply Kirchhoff's Voltage Law (KVL) around loop "aANBba" we would get the following: $$ \mathbb{I}_a \mathbb{Z}_Y - \mathbb{I}_b \mathbb{Z}_Y - \mathbb{V}_{ab} = 0 $$ $$ \mathbb{Z}_Y (\mathbb{I}_a - \mathbb{I}_b) = \mathbb{V}_{ab} \;\;,(where \; \mathbb{V}_{ab} = V_p \angle 0^{\circ} )$$ $$ \mathbb{I}_a - \mathbb{I}_b = \frac{V_p \angle 0^{\circ}}{\mathbb{Z}_Y} \qquad,(Eqn \; 1) $$ However, from all of our previous discussions on balanced 3-phase systems, we know that the line current for phase "b" lags the line current of phase "a" by 120 degrees such that: $$ \mathbb{I}_b = \mathbb{I}_a \angle (-120^{\circ}) $$ Substituting this into equation #1 gives us: $$ \mathbb{I}_a - \mathbb{I}_a \angle (-120^{\circ}) = \frac{V_p \angle 0^{\circ}}{\mathbb{Z}_Y} $$ $$ \mathbb{I}_a (1-1\angle (-120^{\circ})) = \frac{V_p }{\mathbb{Z}_Y} $$ $$ \mathbb{I}_a \Big[ 1-(-\frac{1}{2}) - j\frac{\sqrt{3}}{2} \Big] = \frac{V_p }{\mathbb{Z}_Y} $$ $$ \mathbb{I}_a \Big(\frac{3}{2} + j\frac{\sqrt{3}}{2} \Big) = \frac{V_p }{\mathbb{Z}_Y} $$ $$ \sqrt{3} \; \mathbb{I}_a \angle 30^{\circ} = \frac{V_p }{\mathbb{Z}_Y} $$ $$ \mathbb{I}_a = \frac{V_p }{\mathbb{Z}_Y} \Big( \frac{1}{\sqrt{3} \angle 30^{\circ}} \Big) $$ $$ \mathbb{I}_a = \frac{V_p\angle (-30^{\circ})}{\sqrt{3} \; \mathbb{Z}_Y} = line \; current \; for \; phase "a" $$
The two remaining line currents are determined using the phase sequence (positive in this example): $$ \mathbb{I}_a = \frac{V_p\angle (-30^{\circ})}{\sqrt{3} \; \mathbb{Z}_Y} $$ $$ \mathbb{I}_b = \mathbb{I}_a \angle (-120^{\circ}) $$ $$ \mathbb{I}_c = \mathbb{I}_a \angle 120^{\circ} $$
Alternative method for determining line currents:
We can also obtain the same end results for line currents if we were to transform the source from a delta to Wye configuration as depicted below:
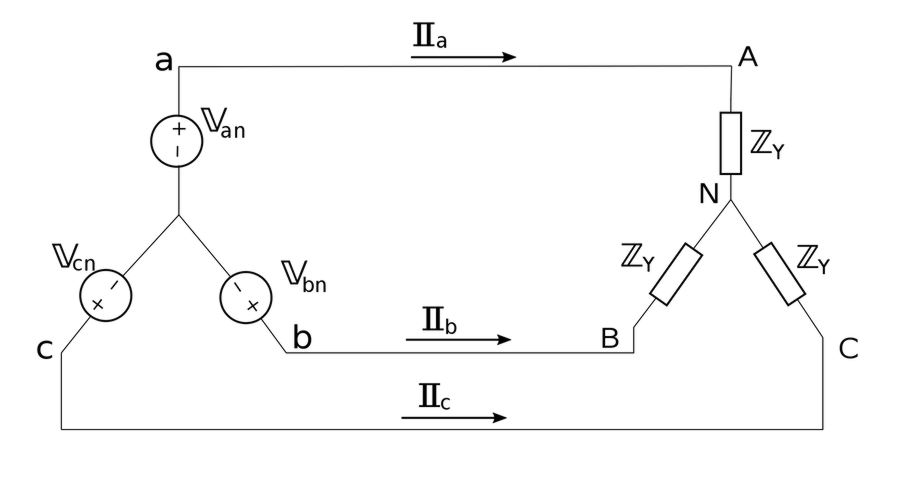
From our previous discussion on Balanced Y-Y connections, we know that: $$ V_p = \frac{V_L}{\sqrt{3}} $$ ...where: $$ V_p = phase \; voltage $$ $$ V_L = line \; voltage $$ In the same section we also learned that phase voltage lags line voltage by 30 degrees such that: $$ \mathbb{V}_{an} = \frac{V_p}{\sqrt{3}} \angle (-30^{\circ}) $$ $$ \mathbb{V}_{bn} = \frac{V_p}{\sqrt{3}} \angle (-150^{\circ}) $$ $$ \mathbb{V}_{cn} = \frac{V_p}{\sqrt{3}} \angle 90^{\circ} $$ From this information we can break the system down into phases and analyze it on a "per-phase" basis. For example, phase "a" is shown below:
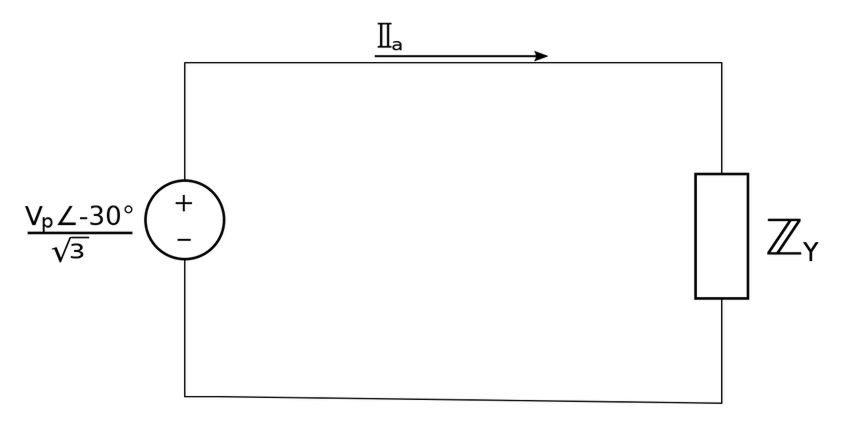
Using Ohm's Law we would get the following expression for the phase current: $$ \mathbb{I}_a = \frac{V_p\angle (-30^{\circ})}{\sqrt{3}} \Big( \frac{1}{\mathbb{Z}_Y} \Big) $$ $$ \mathbb{I}_a = \frac{V_p\angle (-30^{\circ})}{\sqrt{3} \; \mathbb{Z}_Y} $$ This is the same expression we got for the line current of phase "a" using the first method. Additionally, we would proceed to determine the line current for phases "b" and "c" using the phase sequence (positive) just as we did with the first method.
In the next page we will look at an example problem where we analyze a balanced three-phase delta-wye circuit.
Continue on to Balanced Delta-Wye example problem...
