For the following circuit, determine the magnitude of the voltage across each load impedance given the included information:
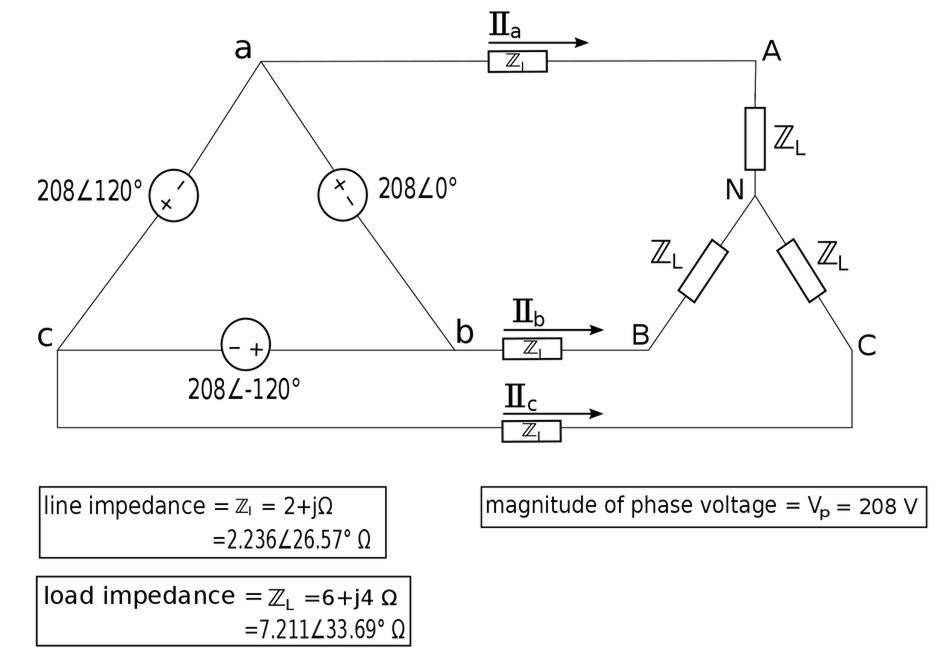
We will begin by applying Kirchhoff's Voltage Law (KVL) around loop "aANBba": $$ -208 + \mathbb{I}_a\mathbb{Z}_l + \mathbb{I}_a\mathbb{Z}_L - \mathbb{I}_b\mathbb{Z}_L - \mathbb{I}_b\mathbb{Z}_l = 0 $$ $$ \mathbb{I}_a(\mathbb{Z}_l + \mathbb{Z}_L) - \mathbb{I}_b(\mathbb{Z}_l + \mathbb{Z}_L) = 208 $$ $$ (\mathbb{Z}_l + \mathbb{Z}_L)(\mathbb{I}_a - \mathbb{I}_b) = 208 \qquad, (Eqn\;1)$$
$$ \mathbb{Z}_l + \mathbb{Z}_L = 2+j+6+j4 = 8+j5 $$ $$ \;\;\;\qquad = 9.434\angle 32.01^{\circ} $$ Plugging this into equation #1 gives us the following:
$$ (9.434\angle 32.01^{\circ}) (\mathbb{I}_a - \mathbb{I}_b) = 208 $$ $$ \mathbb{I}_a - \mathbb{I}_b = 22.05 \angle (-32.01^{\circ}) \qquad,(Eqn\;2) $$
However, we know that the line current for phase "b" lags the line current for phase "a" by 120 degrees such that: $$ \mathbb{I}_b = \mathbb{I}_a \angle (-120^{\circ}) $$ Plugging this new expression for I_b gives us:
$$ \mathbb{I}_a - \mathbb{I}_a \angle (-120^{\circ}) = 22.05 \angle (-32.01^{\circ}) $$ $$ \mathbb{I}_a \Big[1-1\angle (-120^{\circ}) \Big] = 22.05 \angle (-32.01^{\circ}) $$ $$ \mathbb{I}_a \Big[ 1-\Big(-\frac{1}{2} - j\frac{\sqrt{3}}{2}\Big) \Big] = 22.05 \angle (-32.01^{\circ}) $$ $$ \mathbb{I}_a \Big( \frac{3}{2} + j\frac{\sqrt{3}}{2} \Big) = 22.05 \angle (-32.01^{\circ}) $$ $$ \sqrt{3} \; \mathbb{I}_a \angle 30^{\circ} = 22.05 \angle (-32.01^{\circ}) $$
$$ \mathbb{I}_a = 12.73 \angle (-62.01^{\circ}) \; A$$
We now use Ohm's Law to find the voltage across the load impedance (Z_L)for phase "a": $$ \mathbb{V}_{AN} = \mathbb{I}_a \mathbb{Z}_L $$ $$ \qquad = \Big[ 12.73 \angle (-62.01^{\circ}) \Big] \Big[ 7.211\angle 33.69^{\circ} \Big] $$ $$ \mathbb{V}_{AN} = 91.8 \angle (-28.32^{\circ}) \; V $$ Since this is a balanced system, we know that the magnitude of the voltage across a phase of the load is the same for all three phases. Therefore: $$ V_{Load} = |\mathbb{V}_{AN}| $$
$$ V_{Load} = 91.8 \; V $$
