For the following circuit, determine the magnitude of the line currents of the combined loads given a line voltage of 210 V:
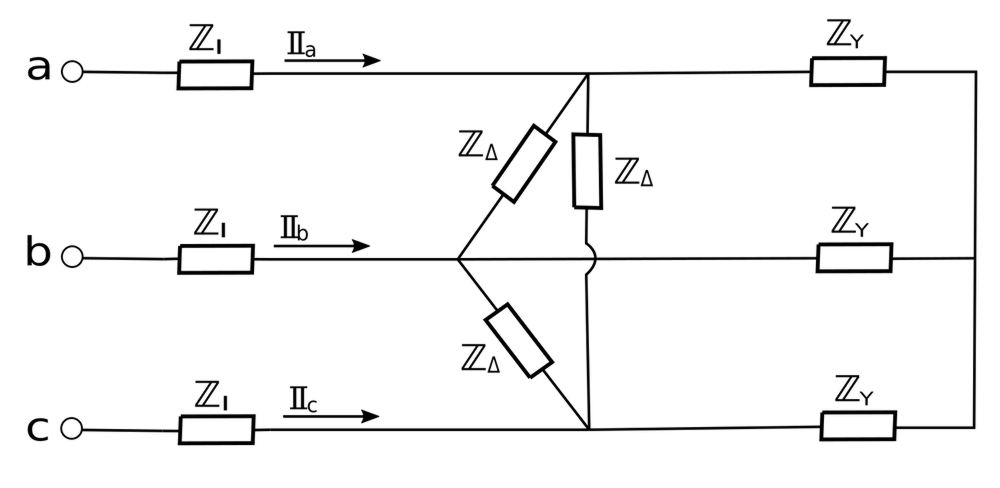
Furthermore, we are given the following impedance values: $$ \mathbb{Z}_l = 1+j \; \Omega = 1.414 \angle 45^{\circ} \; \Omega$$ $$ \mathbb{Z}_{\Delta} = 24-j30 \; \Omega = 38.42 \angle (-51.34^{\circ}) \; \Omega$$ $$ \mathbb{Z}_Y = 12+j5 \; \Omega = 13 \angle 22.62^{\circ} \; \Omega $$
Calculate the phase voltage:
In the section on balanced Y-Y connections, we learned the following relationship between phase and line voltages: $$ V_p = \frac{V_L}{\sqrt{3}} $$ ...where: $$ V_p = magnitude \; of \; phase \; voltage $$ $$ V_L = magnitude \; of \; line \; voltage $$ So, for our circuit above we get: $$ V_p \frac{210}{\sqrt{3}} $$ $$ V_p = 121.2 \; V $$
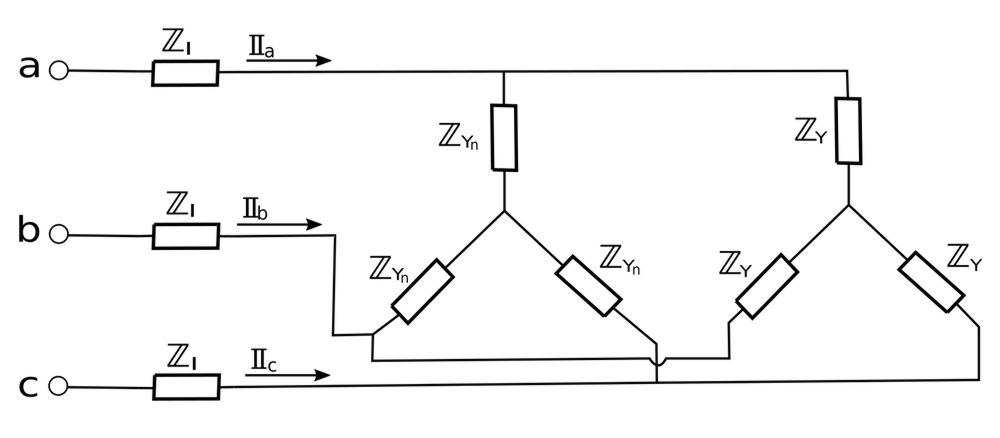
Perform a Delta to Wye Transformation:
We see that the load in our circuit consists of both a delta-connected load and a Y-connected load. To simplify our analysis, we will transform the delta load to a wye. Recall the following expression for the impedance values in a 3-phase Delta-Wye conversion. $$ \mathbb{Z}_{Yn} = \frac{1}{3}\mathbb{Z}_{\Delta} $$ ...where Z_Yn is the impedance value for our newly transformed Y-connected load. For our circuit we will get: $$ \mathbb{Z}_{Yn} = \frac{1}{3} (38.42) \angle (-51.34^{\circ}) $$ $$ \mathbb{Z}_{Yn} = 12.81 \angle (-51.34^{\circ}) \; \Omega$$ We see our newly transformed circuit below:
Per-phase Analysis to determine line current:
Let's take a look at phase "a" (shown below):
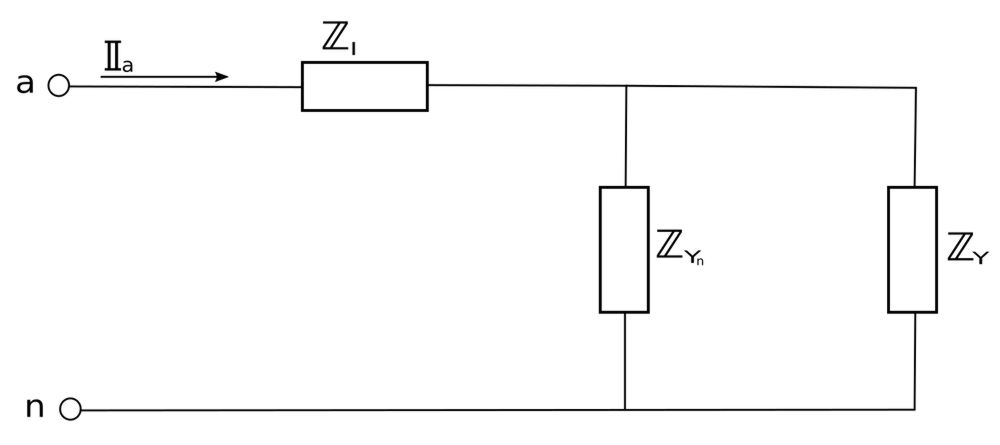
Our goal is to determine the magnitude of the line current for phase "a". We begin by calculating the equivalent impedance for the phase: $$ \mathbb{Z}_{eq} = (\mathbb{Z}_{Yn} || \mathbb{Z}_Y ) + \mathbb{Z}_l$$ $$ \qquad = \frac{1}{\frac{1}{12.81 \angle (-51.34^{\circ})}+\frac{1}{13 \angle 22.62^{\circ}}} + (1+j)$$ $$ \mathbb{Z}_{eq} = 8.875 \angle (-6.772^{\circ}) \; \Omega $$ Recall that for a balanced Y-connected source, the magnitude of the voltages are equal. We already calculated the magnitude of this value above. Since phase "a" is the first phase in our sequence, we know that the phase angle is 0 degrees. (Though it is irrelevant for the purpose of answering the original question.) We can now use Ohm's law to calculate the line current.: $$ \mathbb{I}_a = \frac{\mathbb{V}_p}{\mathbb{Z}_{eq}} = \frac{121.2 \angle 0^{\circ}}{8.875 \angle (-6.772^{\circ})} $$ $$ \qquad = 13.66 \angle 6.772 \; A $$ Remember that the magnitudes of the line currents are equal for all phases. Therefore, if we take the magnitude of the above expression we will get our final answer:
$$ |\mathbb{I}_a| = |\mathbb{I}_{Line}| = 13.66 \; A $$
Continue on to Balanced Delta-Delta Systems...
