Plotting the magnitude and phase of the transfer function is a laborious task. Though we have yet to discuss them, Bode plots are an easier method. Before we address Bode plots however, we need to familiarize ourselves with the concepts of logarithms and decibels as a means of expressing gain.
Properties of Logarithms:
Let's first recall the following properties of logarithms: $$ 1) \; \log AB = \log A + \log B $$ $$ 2) \; \log \frac{A}{B} = \log A - \log B $$ $$ 3) \; \log A^n = n\log A $$ $$ 4) \; \log 1 = 0 $$ A more complete list of logarithmic properties can be found here
Bels/Decibels:
The bel
In communications systems, gain is usually measured in units of bels. A bel is a logarithmic expression of the ratio of two levels of power or power gain (G). $$ G = \# \; of \; bels $$ Mathematically it is defined as: $$ G = \log_{10} \frac{P_2}{P_1} $$ ...where P1 and P2 are the two power levels being measured/compared
The decibel
For many real-world purposes, a bel is a rather large quantity of measurement. For this reason, a unit of lower magnitude (the decibel) is often used. $$ 1 \; decibel = \frac{1}{10} \; bel $$ Therefore, power gain in decibels is expressed as:
Power gain (in decibels):
$$ G_{dB} = 10\log_{10} \Big( \frac{P_2}{P_1} \Big) \qquad,(Eqn\;1) $$
Examples:
1) When: $$ P_1=P_2 $$ $$ G_{dB} = 0 \; dB $$ 2) When: $$ P_2=2P_1 $$ $$ G_{dB} = 10\log_{10}2 \approx 3\;dB $$ 3) When: $$ P_2=0.5P_1 = \frac{1}{2}P_1$$ $$ G_{dB} = 10\log_{10}\Big( \frac{1}{2} \Big) \approx -3\;dB $$ If you look at examples 2 and 3 you notice that the logarithm of the reciprocal of a value equals the negative of the logarithm of that value.
Voltage and Current Gain:
Gain can also be measured in terms of a voltage or current ratio. Consider the following circuit/network:
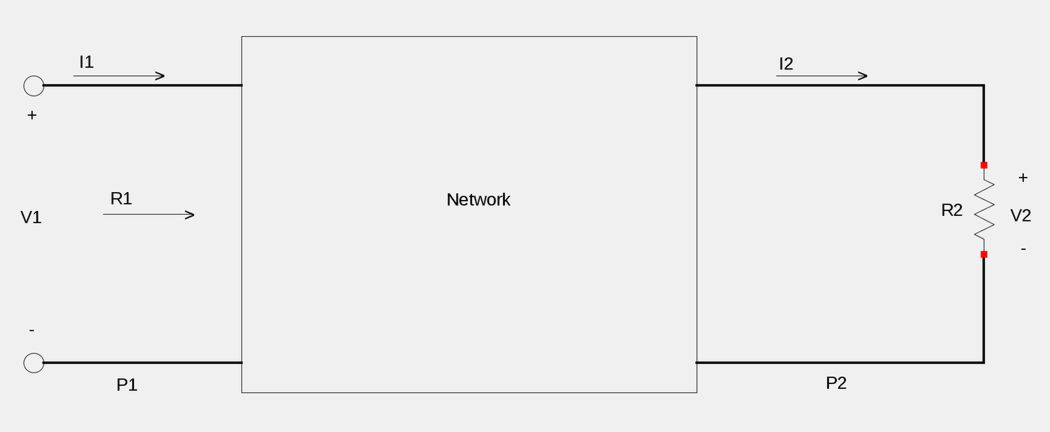
For the above figure: $$ P_1 = input \; power $$ $$ P_2 = output \; (load) \; power $$ $$ R_1 = input \; resistance $$ $$ R_2 = load \; resistance $$ Recall that power can be defined as: $$ P = \frac{V^2}{R} $$ So, for our circuit above, we have: $$ P_1 = \frac{V_1^2}{R_1} \qquad. P_2 = \frac{V_2^2}{R_2} $$ By equation #1 we have: $$ G_{dB} = 10\log_{10} \frac{P_2}{P_1} $$ $$ \quad \;\;\; = 10\log_{10} \Big( \frac{\frac{V_2^2}{R_2}}{\frac{V_1^2}{R_1}} \Big) $$ $$ \quad \;\;\; = 10\log_{10} \Big( \frac{V_2^2 R_1}{V_1^2 R_2} \Big) $$ ...and by the properties of logarithms (division), we have: $$ G_{dB} = 10\log_{10} V_2^2R_1 - 10\log_{10} V_1^2R_2 $$ Now using the multiplication property of logarithms, we have: $$ \quad \;\;\; = (10\log_{10} V_2^2+10\log_{10}R_1)-(10\log_{10} V_1^2+10\log_{10} R_2) $$ $$ \quad \;\;\; = (10\log_{10} V_2^2-10\log_{10} V_1^2)+(10\log_{10}R_1-10\log_{10} R_2) $$ Again, we use the division property of logarithms: $$ G_{dB} = 10\log_{10} \Big( \frac{V_2}{V_1} \Big)^2 + 10\log_{10} \Big( \frac{R_1}{R_2} \Big) $$ Finally, using the exponent property of logarithms gives us: $$ G_{dB} = 20 \log_{10} \Big( \frac{V_2}{V_1} \Big) + 10\log_{10} \Big( \frac{R_1}{R_2} \Big) \qquad,(Eqn\;2) $$ When we are comparing two voltage levels, it is usually assumed that: $$ R_1 = R_2 $$ ...and under this assumption, equation #2 becomes: $$ G_{dB} = 20 \log_{10} \Big( \frac{V_2}{V_1} \Big) + 10\log_{10}1 $$ Knowing that log of 1 = 0 gives us:
Voltage gain (in decibels):
$$ G_{dB} = 20 \log_{10} \Big( \frac{V_2}{V_1} \Big) \qquad,(Eqn\;3)$$
If we were to repeat all of the above steps with the power values expressed as: $$ P_1 = I_1^2R_1 \qquad, P_2 = I_2^2R_2 $$ and make the same assumption that: $$ R_1 = R_2 $$ ...we would arrive at the following expression:
Current gain (in decibels):
$$ G_{dB} = 20 \log_{10} \Big( \frac{I_2}{I_1} \Big) \qquad,(Eqn\;4)$$
Equations 3 and 4 are only used with voltage and current magnitudes. Negative signs and phase angles are handled separately (yet to be discussed).
Decibels and the transfer function:
If you examine equations 1, 3 and 4, you see that a decibel value is a logarithmic expression of the ratio of two values that are of the SAME TYPE. For this reason, decibels can be used to express the transfer functions for voltage and current gain: $$ \mathbb{H}(\omega) = \frac{\mathbb{V}_o(\omega)}{\mathbb{V}_i(\omega)} = voltage \; gain $$ $$ \mathbb{H}(\omega) = \frac{\mathbb{I}_o(\omega)}{\mathbb{I}_i(\omega)} = current \; gain $$ HOWEVER, decibels CANNOT be used to express the transfer functions for impedance and admittance since those expressions involve values of two different types: $$ \mathbb{H}(\omega) = \frac{\mathbb{V}_o(\omega)}{\mathbb{I}_i(\omega)} = transfer \; impedance $$ $$ \mathbb{H}(\omega) = \frac{\mathbb{I}_o(\omega)}{\mathbb{V}_i(\omega)} = transfer \; admittance $$
Now that we understand the decibel scale, lets take a look at Bode plots:
Continue on to Intro to Bode plots...
