A complex number "z" can be expressed in three forms:

1) Rectangular form:

$$ z = x + jy $$ where: $$j = \sqrt{-1}$$ $$ x = \; "real \; part" $$ $$ y = \; "imaginary \; part" $$ Remember that x and y represent real and imaginary parts of z when graphed in the complex plane.

2) Polar Form:

$$ z = r \angle \phi $$ where: $$ r = magnitude \; of z $$ $$ \phi = phase \; of \; z $$

3) Exponential Form:

$$z = re^{j\phi}$$

Converting between complex numbers in rectangular and polar form:

A complex number "z" graphed in the complex plane is shown below:

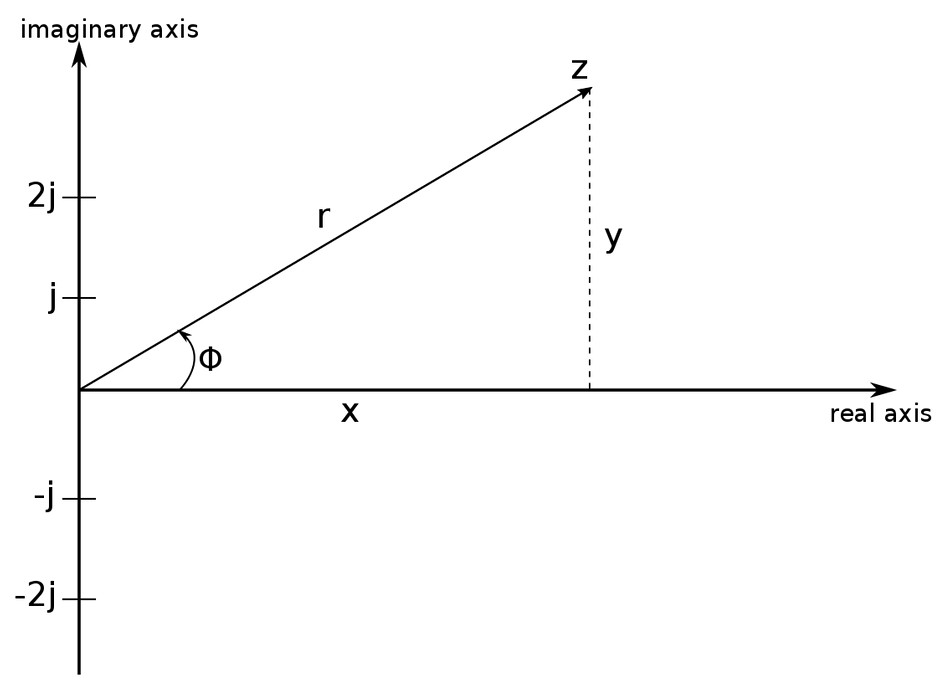
Converting from rectangular to polar form:

We notice that "r" is the magnitude of the complex number "z". Using Pythagorean's theorem, we can determine "r" as being: $$ r = \sqrt{x^2 + y^2} $$ Also, by the definition of the tangent of an angle: $$\phi = tan^{-1} \Big( \frac{y}{x} \Big)$$

Converting from polar to rectangular form

Using the definition of sine and cosine of an angle gives us: $$ x = rcos \phi $$ $$ y = rsin \phi $$

When working with complex numbers, it is useful to keep in mind the basic properties of mathematical operations performed on them:

Properties of Complex Numbers:

given two complex numbers (z1 and z2) shown below in rectangular and polar form: $$ z_1 = x_1 + jy_1 = r_1 \angle \phi_1$$ $$ z_2 = x_2 + jy_2 = r_2 \angle \phi_2 $$

1) Addition: $$ z_1 + z_2 = (x_1 + x_2) + j(y_1+y_2) $$ 2) Subtraction: $$ z_1 - z_2 = (x_1 - x_2) + j(y_1-y_2) $$ 3) Multiplication: $$ z_1 z_2 = r_1 r_2 \angle(\phi_1 + \phi_2) $$ 4) Division: $$ \frac{z_1}{z_2} = \frac{r_1}{r_2} \angle(\phi_1-\phi_2) $$ 5) Reciprocal: $$ \frac{1}{z} = \frac{1}{r} \angle(-\phi) $$ note that: $$\frac{1}{j} = -j$$ 6) Square Root: $$ \sqrt{z} = \sqrt{r} \angle \Big( \frac{\phi}{2} \Big)$$ 7) Complex Conjugate: $$ z^* = (x-jy) = r \angle(-\phi) $$ $$ = re^{-j\phi} $$

Let's take a quick look at some example problems involving complex numbers:

Continue on to Complex Number Problems....