Ex 1) Convert the following sinusoid to phasor notation:

$$v(t)=-4\sin (30t+{50}^{\circ })$$

Step 1) Express the sinusoid in positive cosine form so that it can be written as the real part of a complex number.

We will use the graphical approach in order to convert the sine function having a negative amplitude into a cosine function having a positive amplitude:

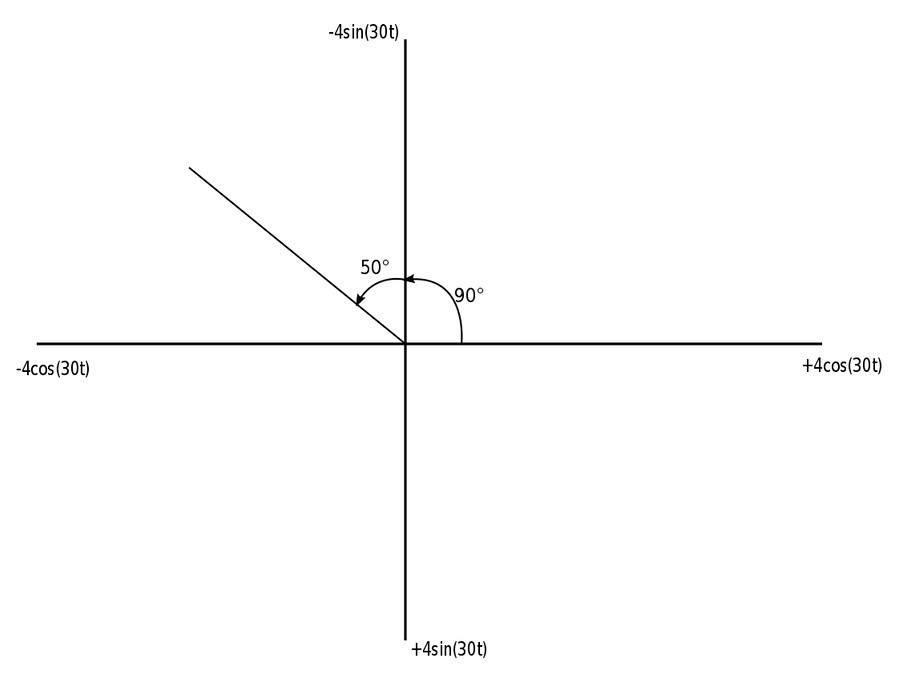
From the graph above we can see that: $$-4\sin (30t+{50}^{\circ })=4\cos (30t+{50}^{\circ }+{90}^{\circ })$$ Therefore: $$v(t)=4\cos (30t+{140}^{\circ })$$ And from our previous explanation of phasor notation we know that: $$v(t)=R_e\{4e^{j(30t+{140}^{\circ })}\}$$ $$=R_e\{4e^{j30t}{e}^{j{140}^{\circ }}\}(Expression1)$$

Step 2) Remove the time factor from expression #1. Whatever is left is the phasor.

Now recall Expression #4 from the previous page $$\mathbb{V}=V_m{e}^{j\varphi }$$ and apply it to the expression #1 to give us the following: $$\mathbb{V}=4e^{j{140}^{\circ }}(Expression2)$$ Notice that the e^(jwt) term (e^(j30t) in this case) has been removed.

Converting expression #2 to polar form gives us: $$\mathbb{V}=4\mathrm{\angle }{140}^{\circ }$$

Ex 2) Convert the following sinusoid to phasor notation:

$$v(t)=-8\cos (16t+{15}^{\circ })$$

Step 1) Express the sinusoid in positive cosine form so that it can be written as the real part of a complex number.

We will once again use the graphical approach to convert this cosine function having a negative amplitude into a cosine function having a positive amplitude.

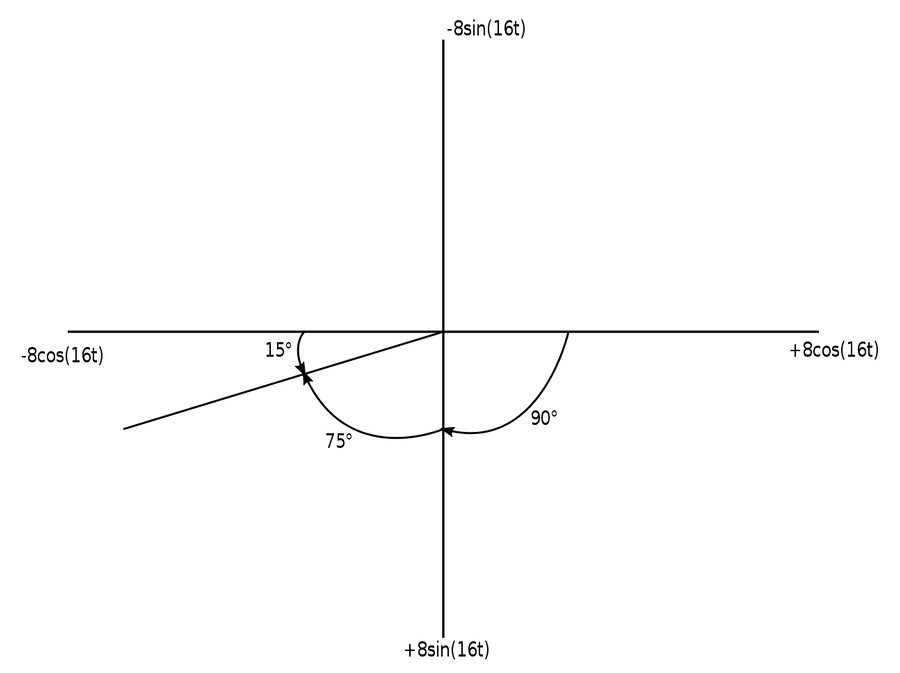
From the above graphical illustration we can see that: $$-8\cos (16t+{15}^{\circ })=8\cos (16t-{165}^{\circ })$$ ...and when we express this as the real part of a complex number we get: $$v(t)=R_e\{8e^{j(16t-{165}^{\circ })}\}$$ or: $$v(t)=R_e\{8e^{j16t}{e}^{j(-{165}^{\circ })}\}(Expression3)$$

Step 2) Remove the time factor from expression #3. Whatever is left is the phasor.

Now recall Expression #4 from the previous page $$\mathbb{V}=V_m{e}^{j\varphi }$$ and apply it to the expression #3 to give us the following: $$\mathbb{V}=8e^{j(-{165}^{\circ })}(Expression4)$$ Notice that the e^(jwt) term (e^(j16t) in this case) has been removed.

Converting expression #4 to polar form gives us: $$\mathbb{V}=8\mathrm{\angle }(-{165}^{\circ })$$

Now let's look a some example problems that go the other way and convert phasors to sinusoids.

Continue on to Converting phasors to sinusoids....