Example 1:

Given the following sinusoid, $$ 45cos(5 \pi t + 36^{\circ}) $$ ...calculate the amplitude, phase, angular frequency, period and frequency.

From our previous discussion of sinusoids we can easily see that Amplitude = 45 and the phase is 36 degrees. Also note that: $$ angular \; frequency = \omega = 5\pi $$ also: $$ \omega = 2\pi f = \frac{2\pi}{T}$$ ...where T is the period of the sinusoid. Therefore by rearranging the above equation: $$ T = \frac{2\pi}{\omega} $$ $$ T = \frac{2\pi}{5\pi} $$

$$ T = 400 ms = period$$

We also know that: $$ f = frequency = \frac{1}{T} $$ therefore: $$ f = \frac{1}{400ms} $$

$$ f = 2.5Hz = frequency$$

Example 2:

Calculate the phase angle between: $$ v_1 = -10cos(\omega t + 50^{\circ}) $$ $$ v_2 = 12sin(\omega t - 10^{\circ}) $$ ...using both the method of trig identities and the graphical approach. Determine which sinusoid is leading.

Method #1 (trig identities)

We start by expressing both sinusoids in sine form with positive amplitudes (v2 is already in this form): $$ v_1 = -10cos(\omega t + 50^{\circ}) $$ Using our trig identities: $$ v_1 = 10sin(\omega t + 50^{\circ} - 90^{\circ}) $$ $$ v_1 = 10sin(\omega t - 40^{\circ}) $$ and: $$ v_2 = 12sin(\omega t - 10^{\circ}) $$ From this we can see that the phase difference is 30 degrees

$$\phi = 30^{\circ}$$

The negative signs in front of the phase angles indicate a rightward shift graphically. Since v1 is shifted farther to the right than v2, its starting point occurs later in time (relative to v2). This means that:

$$v2 \; "leads" \; v1 \; by \; 30 \; degrees.$$

Method #2 (Graphical Approach)

Start by plotting v1 and v2 on our "improvised" coordinate system:

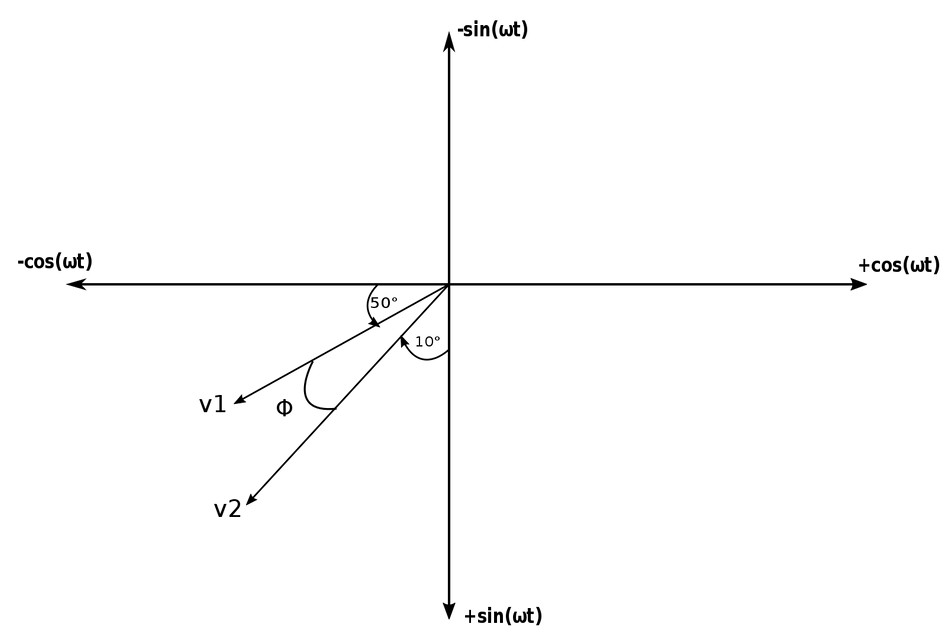
From inspection we can see that:

$$ \phi = 30^{\circ} $$

We also again notice that v2 "leads" v1 by 30 degrees.

Now that we have a decent understanding of sinusoids, let's also briefly review complex numbers.

Continue on to Review of complex numbers....