Consider the following expression which represents a sinusoidal voltage as a function of time: $$v(t) = V_msin(\omega t)$$ ...where: $$V_m = amplitude \; of \; sinusoid$$ $$\omega = angular \; frequency \; (in \; radians) $$ $$(\omega t) = argument \; of \; the \;sinusoid $$ While this is meant to be a brief review of sinusoids and not a "bottom-up" explanation of trigonometric functions, recall that a sinusoid repeats itself every "T" seconds where: $$T = period \; of \; function $$ The frequency (f) of a sinusoidal function is the number of cycles per second that it repeats and is expressed in hertz. Frequency is the inverse of period: $$f = \frac{1}{T} $$ Angular frequency (expressed in terms of radians per second) is represented as: $$\omega = 2 \pi f $$

A periodic function satisfies the following expression for all values of "T" and all integers "n": $$f(t) = f(t+nT) $$

General expression for a sinusoid:

More generally, we can represent a sinusoid as: $$v(t) = V_m sin(\omega t + \phi) $$ ...where: $$\phi = phase \; of \; sinusoid $$ $$(\omega t + \phi) = argument \; of \; sinusoid $$

Consider the following two sinusoids: $$v_1(t) = V_m sin(\omega t) $$ $$v_2(t) = V_m sin(\omega t + \phi) $$ ...which are shown below plotted on the same graph (blue = v1, red = v2, x-axis is in terms of time "t"):

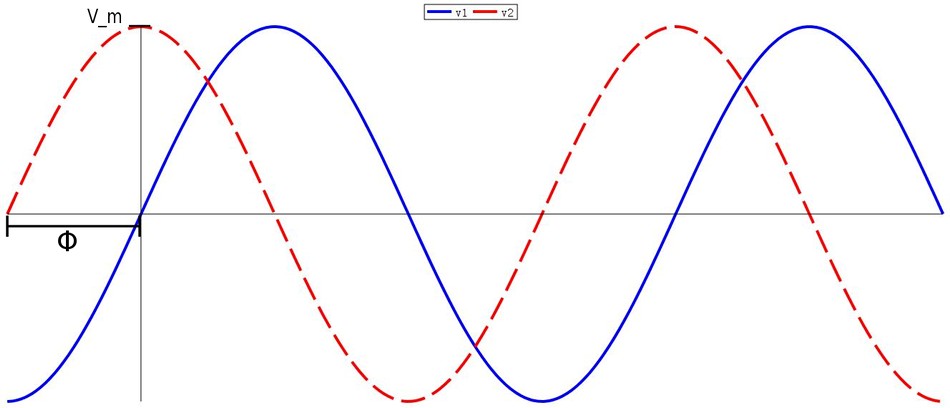
From the graph we can see that the starting point of v2 occurs 1st in time relative to v1. In other words: $$v_2 \; "leads" \; v_1 \; by \; \phi. $$ ...which also means that: $$v_1 \; "lags"\; v_2 \; by \; \phi. $$ Also , if: $$\phi \ne 0 $$ then v1 and v2 are "out of phase."

Comparing multiple sinusoids:

A sinusoid can be expressed in either sine or cosine form. However, when comparing two sinusoids, it is convenient to express both as either sine or cosine with positive amplitudes. This can be done via trigonometric identities or a graphical approach.

Using trig identities to compare multiple sinusoids:

Recall the following two trig identities: $$1) \; sin(A \pm B) = sinAcosB \pm cosAsinB $$ $$2) \; cos(A \pm B) = cosAcosB \mp sinAsinB $$

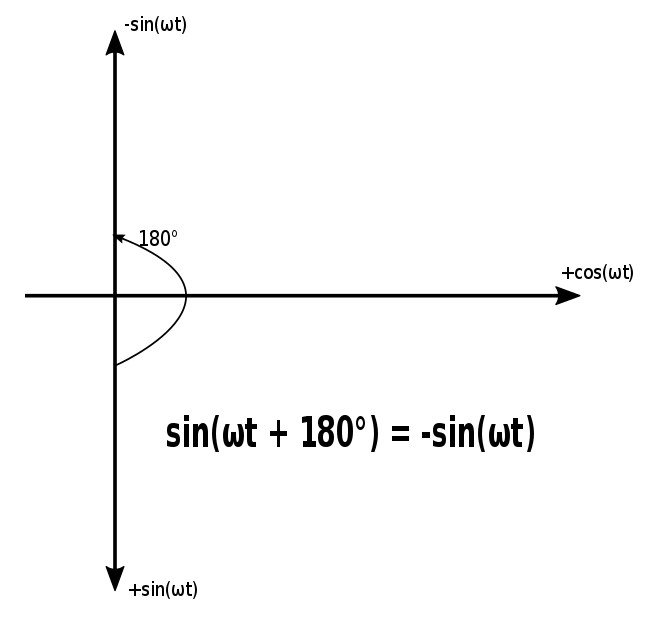
The above two identities can be used to show that the following are true: $$sin(\omega t \pm 180 ^{\circ}) = -sin(\omega t) $$ $$cos(\omega t \pm 180 ^{\circ}) = -cos(\omega t) $$ $$sin(\omega t \pm 90 ^{\circ}) = \pm cos(\omega t) $$ $$cos(\omega t \pm 90 ^{\circ}) = \mp sin(\omega t) $$ The above four relationships allow us to transform a sinusoid from sine to cosine and vice versa.

Using a graphical approach to relate/compare sinusoids:

We can also compare sinusoids that are expressed as sines and cosines with a graphical approach. With this method, the horizontal axis represents the magnitude of cosine and the vertical axis represents the magnitude of sine. Unlike a traditional Cartersian plane the positive direction of sine is denoted as pointing "downwards" here. (Don't get confused by this). Furthermore, angles are measured positively in a counter-clockwise direction from the horizontal axis.

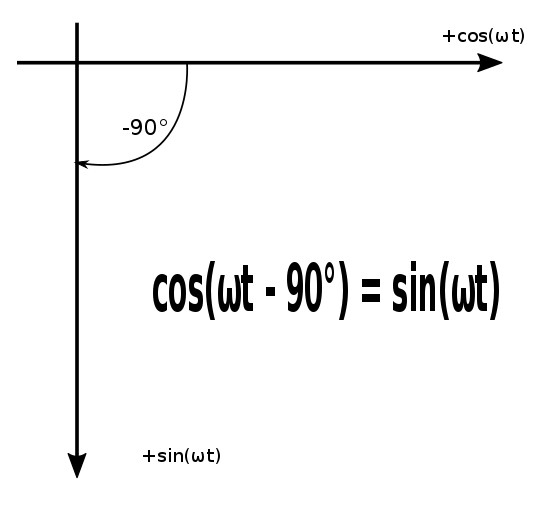
Another illustration of the graphical approach

Using the Graphical Method to Add/Subtract Sinusoids of the Same Frequency:

Assume that we want to add the following two sinusoids (v1 and v2): $$ v_1(t) = Acos(\omega t) $$ $$ v_2(t) = Bsin(\omega t) $$ The magnitude and argument of the resulting sinusoid can be obtained from the following triangle:

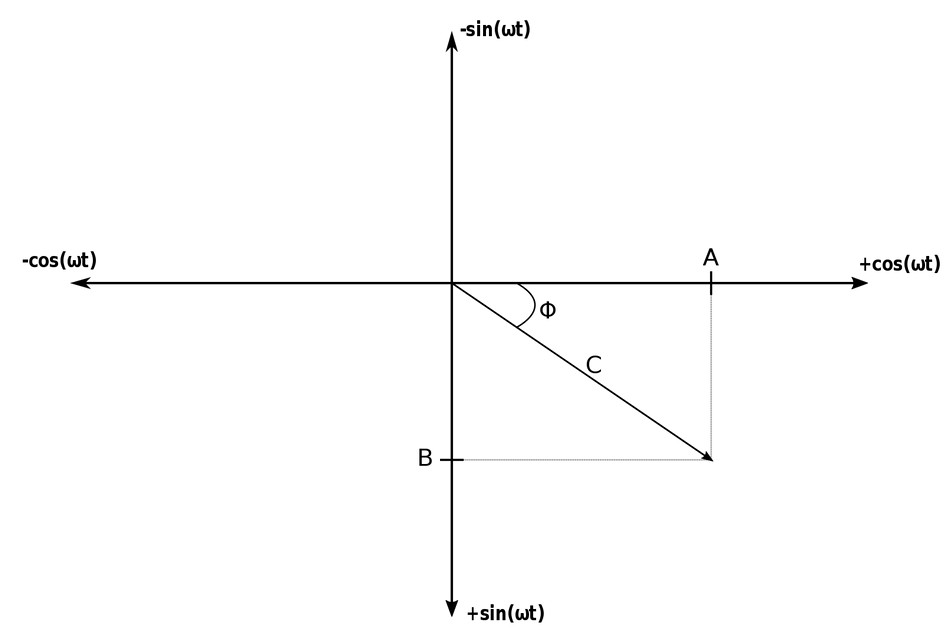
Using Pythagorean's Theorem we determine that: $$C = magnitude \; of \; resultant \; sinusoid $$ $$ = \sqrt{A^2+B^2} $$ The phase angle can be determined by the definition of tangent $$ tan(\phi) = \frac{B}{A} $$ $$ \phi = tan^{-1} \Big(\frac{B}{A} \Big) $$ For the phase angle, don't forget the difference between a reference angle (relative to the horizontal axis) and the actual angle. The sign of A and B will tell you what quadrant of the plane the angle lies.

Example: Sum the following sinusoids:

$$ 3cos(\omega t) - 4sin(\omega t) $$ Start by using the graphical approach to plot the sinusoids:

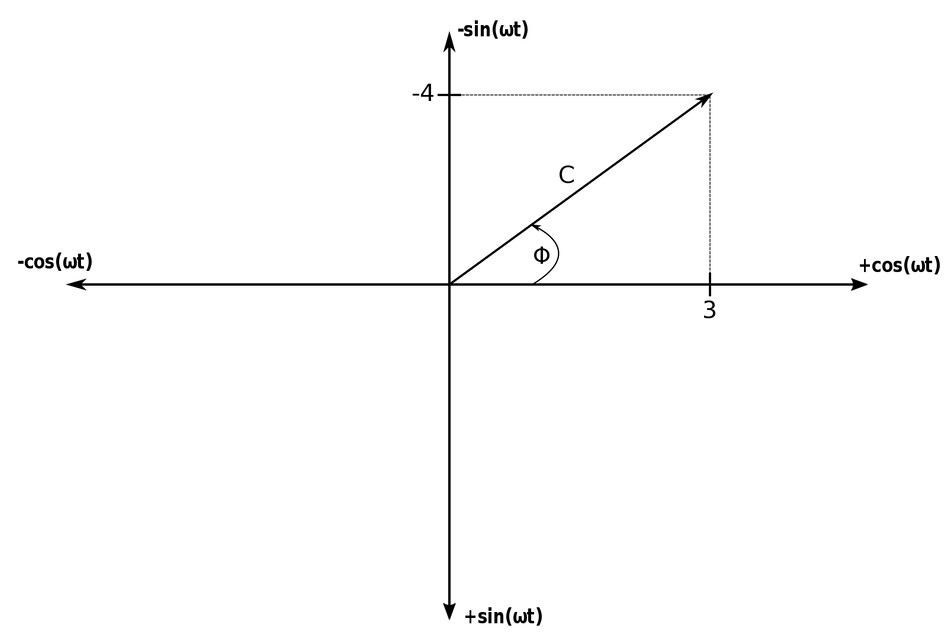
$$ C = magnitude \; of \; resulting \; sinusoid $$ $$ C = \sqrt{(-4)^2 + 3^2} $$ $$ C = 5 $$ $$ tan(\phi) = \frac{4}{3} $$ $$ \phi = tan^{-1} \Big( \frac{4}{3} \Big) $$ $$ \phi = 53.1^{\circ} $$ Remember that the sign convention of this graphical approach is not the same as a traditional Cartersian coordinate system. Therefore, when you obtain a reference angle, the actual angle is determined by the signs of the magnitudes of each individual sinusoid. Using these positive or negative signs, you then determine which quadrant the reference angle lies in. In this case it is in the first quadrant and is 53.1 degrees from positive cosine in the positive direction (counter-clockwise). Therefore: $$ 3cos(\omega t) - 4sin(\omega t) = 5cos(\omega t + 53.1^{\circ}) $$

Let's quickly look at some example problems involving sinusoids.

Continue on to Sinusoid example problems...