(Example 1) Express the following phasor as a sinusoid:

$$ \mathbb{V} = -3 + j4 $$ We will first convert the phasor from rectangular form to exponential form. The magnitude of the phasor is: $$ r = \sqrt{x^2+y^2} $$ $$ r = \sqrt{(-3)^2+4^2} $$ $$ r = 5 $$ The phase angle is defined as: $$ \phi = tan^{-1} \Big( \frac{y}{x} \Big) $$ Our reference angle will be: $$ \phi_{ref} = tan^{-1} \Big( \frac{4}{3} \Big)$$ $$ \phi_{ref} = 53.13^{\circ} $$ Since our x-value is negative and our y-value positive, the actual angle will fall in the 2nd quadrant (180 - 53.13 degrees). $$ \phi = 180^{\circ} - 53.13^{\circ} = 126.9^{\circ} $$ We can now express the phasor in polar notation: $$ \mathbb{V} = 5 \angle (126.9^{\circ}) $$ Which is equivalent to the following expression in exponential form: $$\mathbb{V} = 5e^{j126.9^{\circ}} $$ Now follow the steps explained in the introduction to phasor notation page in order to get the corresponding sinusoid.

Multiply the phasor by e^(jwt) and take the real part:

$$ v(t) = R_e \{ 5e^{j126.9^{\circ}} e^{j\omega t} \}$$ $$ v(t) = R_e \{ 5e^{j(\omega t + 126.9^{\circ})} \} \qquad(Expression \; 1) $$

Recall Euhler's Identity: $$ e^{j\phi} = \cos \phi + j \sin \phi $$ ...and use it to convert the complex number in expression #1 from exponential form to rectangular form having a real and imaginary part:

$$ v(t) = R_e \{ 5\cos(\omega t + 126.9^{\circ}) + 5j \sin(\omega t + 126.9^{\circ}) \} $$

Final Answer:

$$ v(t) = 5\cos(\omega t + 126.9^{\circ}) $$

(Example 2) Express the following phasor as a sinusoid:

$$ \mathbb{V} = j8e^{-j20^{\circ}} $$ We recognize that the phasor is two complex numbers multiplied together. Complex numbers are easier to multiply when they are expressed in polar form. Converting "j" to polar form may seem odd at first so let's look at it graphed in the complex plane:

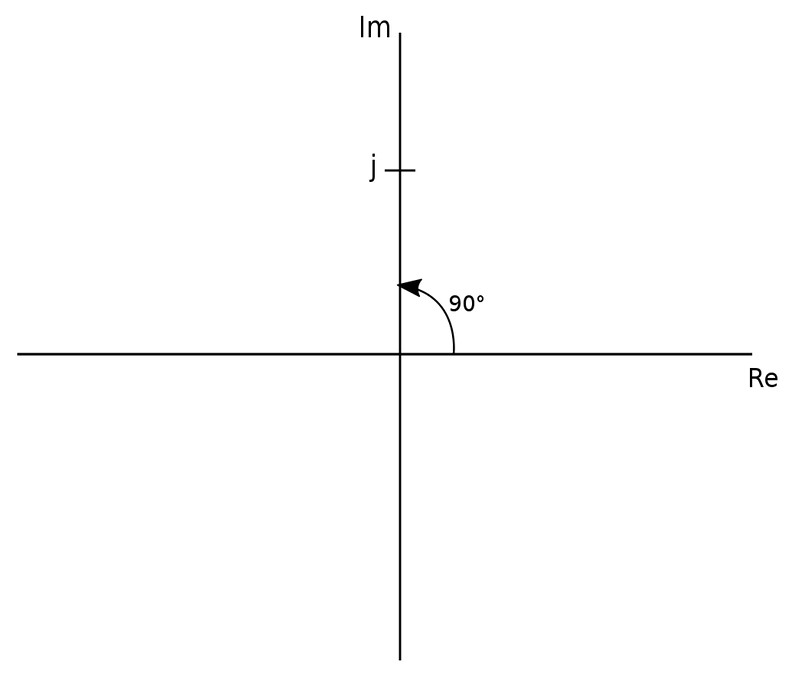
Hopefully you can easily see that the magnitude is 1 and the angle is 90 degrees. This means that "j" in polar form can be expressed as: $$ 1 \angle 90^{\circ} $$ From the previous page that covered complex numbers we recognize that we can express the 2nd complex number as: $$ 8 \angle (-20^{\circ}) $$ Therefore, our phasor expressed in polar form is: $$ \mathbb{V} = (1 \angle 90^{\circ})(8 \angle (-20^{\circ})) $$

Recall the definition for multiplication of two complex numbers: $$ z_1 z_2 = r_1 r_2 \angle(\phi_1 + \phi_2) $$ ...and apply it to our phasor above:

$$ \mathbb{V} = 1(8) \angle (90^{\circ} - 20^{\circ}) $$ $$ \mathbb{V} = 8 \angle 70^{\circ} $$ Expressing this in exponential form gives us: $$\mathbb{V} = 8e^{j70^{\circ}} $$ Once again we follow the steps explained in the introduction to phasor notation page in order to get the corresponding sinusoid.

Multiply the phasor by e^(jwt) and take the real part:

$$ v(t) = R_e \{ 8e^{j70^{\circ}} e^{j\omega t} \} $$ $$ v(t) = R_e \{ 8e^{j(\omega t + 70^{\circ})} \} \qquad(Expression \; 2)$$

Recall Euhler's Identity: $$ e^{j\phi} = \cos \phi + j \sin \phi $$ ...and use it to convert the complex number in expression #2 from exponential form to rectangular form having a real and imaginary part:

$$ v(t) = R_e \{ 8\cos(\omega t + 70^{\circ}) + 8j\sin(\omega t + 70^{\circ}) \} $$

Final Answer:

$$ v(t) = 8\cos(\omega t + 70^{\circ}) $$

Another useful application of phasors involves finding the derivatives and integrals of sinusoids. In the next section we will look at such applications.

Continue on to Phasors and sinusoidal calculus....