Phasor Notation/Representation is based on Euhler's Identity which states the following: $$ e^{\pm j\phi} = cos(\phi) \pm jsin(\phi) $$ Notice that cosine(phi) and sine(phi) are the real and imaginary parts of the complex number: $$ cos(\phi) = R_e\{e^{j\phi}\} \qquad(eqn \; 1) $$ $$ sin(\phi) = I_m\{ e^{j\phi} \} \qquad(eqn \; 2) $$ Either equation 1 or equation 2 can be used to develop a phasor, but standard convention is to use equation #1 (the cosine term).
Developing the phasor notation:
Given the following sinusoid: $$ v(t) = V_mcos(\omega t + \phi) $$ By equation #1 we can rewrite this as: $$ v(t) = R_e \{ V_me^{j(\omega t + \phi)} \} $$ and by rules of exponentials: $$ = R_e \{ V_me^{j\omega t}e^{j\phi} \} \qquad(Eqn 3)$$
Now let us define the following expression: $$ \mathbb{V} = V_me^{j\phi} \qquad(expression \; 4)$$ ...and recall the following expression for converting a complex number "z" from exponential form to polar form: $$ z = re^{j\phi} = r\angle \phi $$ ...which means that expression #4 can be expanded in the following manner: $$ \mathbb{V} = V_me^{j\phi} = V_m \angle \phi \qquad(expression \; 5)$$ Using expression #5, we can now rewrite equation #3 as the following:
$$ v(t) = R_e \{ \mathbb{V}e^{j\omega t} \} \qquad(expression \; 6)$$ where the term "sinor" is defined as the following: $$ \mathbb{V}e^{j\omega t} = V_me^{j(\omega t + \phi)} $$
Oftentimes the phasor representation of the sinusoid v(t) is simply expressed as: $$ \mathbb{V} $$ ,where the "double V" is a complex representation of the magnitude and phase of a sinusoid. Whenever a sinusoid is expressed in such a manner, the e^{jwt} portion is always assumed to be present. It is important to not forget this because omega represents angular frequency and cannot be ignored.
To get the sinusoid corresponding to a phasor:
$$ multiply \; the \; phasor \; (\mathbb{V}) \; by \; e^{j\omega t} $$ $$ \qquad \qquad where \; \mathbb{V} = V_me^{j\phi} = V_m \angle \phi $$ ...and then take the real part of the result.
To get the phasor that corresponds to a sinusoid:
- Express the sinusoid in cosine form so that it can be written as the real part of a complex number.
- Remove the following time factor: $$e^{j\omega t} $$ and whatever is left is the phasor.
By suppressing the time factor, e^(jwt), the sinusoid is transformed from the time domain to the phasor domain.
$$ v(t) = V_mcos(\omega t + \phi) ,(time\;domain) $$ when transformed to the phasor domain is equivalent to $$\mathbb{V} = V_m \angle \phi ,(phasor\;domain)$$
In the phasor domain, the suppressed time factor, e^(jwt), is also known as the "frequency factor". Although it is often not implicitly shown, the response, v(t), depends on frequency and for that reason the phasor domain is also referred to as the "frequency domain."
In order to better understand expressions 5 and 6, consider the plot of the sinor in expression #6 on the complex plane:
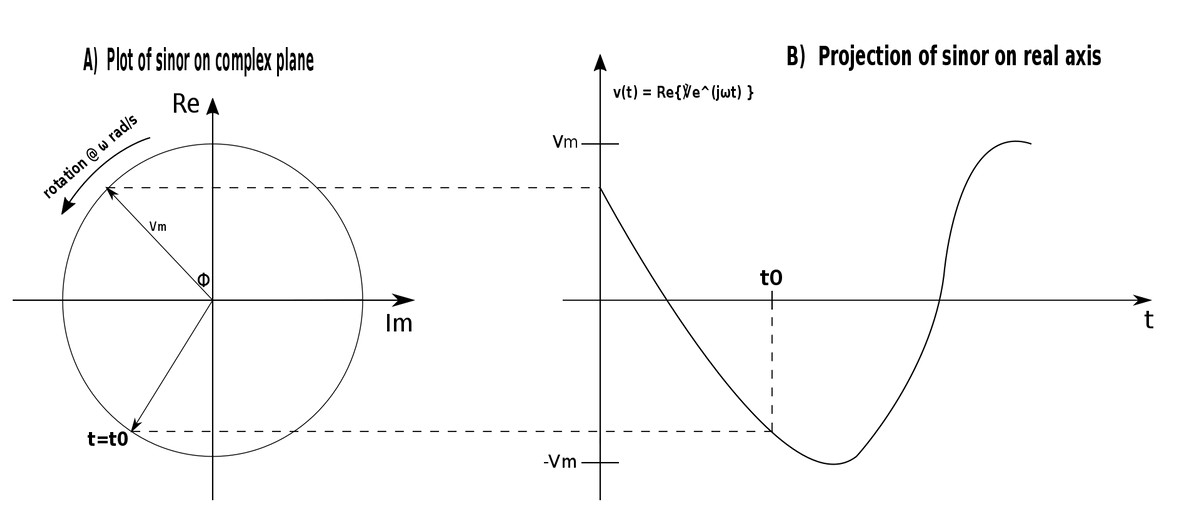
For the plot of the sinor (graph A) as time increases, the phasor rotates on a circle with radius Vm at an angular velocity of omega in the counter-clockwise direction. In graph B, v(t) is the projection of the sinor on the real axis. At time t=t0, the value of the sinor is equal to the phasor of the sinusoid v(t).
| Key differences between sinusoids and phasors: | |
|---|---|
| sinusoid, v(t) | $$ Phasor, \mathbb{V} $$ |
| "Instantaneous" or "time-domain" representation | "Frequency" or "Phasor-domain" representation |
| Time-dependent | Not time-dependent |
| Always real with no complex terms | Generally complex |
Before continuing, we will first look at some problems that require us to convert a sinusoid to phasor form:
Continue on to Converting sinusoids to phasors....
