Consider a three-phase circuit having the following properties:
$$ load \; impedance = \mathbb{Z}_L = 20+j10 = 22.36\angle 26.57^{\circ} \; \Omega$$ $$ line \; impedace = 480 \; V \; (RMS) $$
Calculate the average/real power (P) delivered to the load if:
A) the 3-phase load is delta-connected
B) the 3-phase load is Y-connected
A) The load is delta-connected:
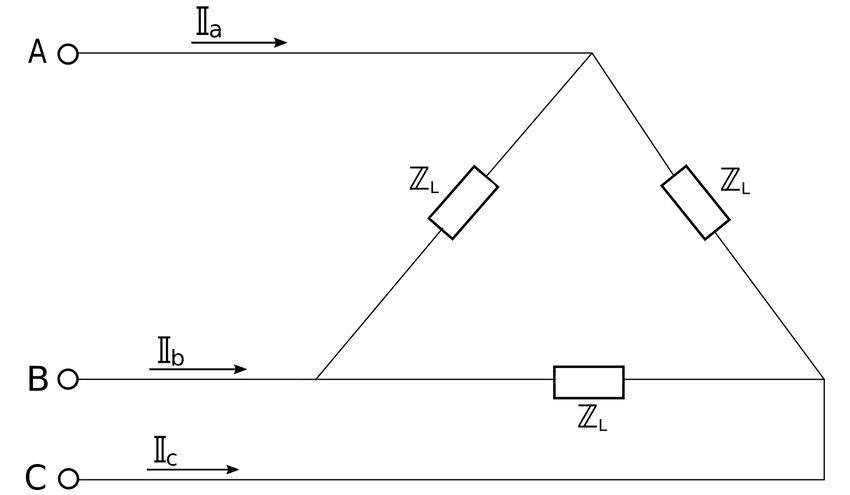
When the load is delta connected, line voltage is equal to phase voltage: $$ V_p = V_L $$ Additionally, the phase current is defined as: $$ \mathbb{I}_p = \frac{\mathbb{V}_p}{\mathbb{Z}_L} = \frac{\mathbb{V}_L}{\mathbb{Z}_L} $$ Therefore, the phase current for phase "AB" (assume positive rotation) is defined as: $$ \mathbb{I}_{AB} = \frac{480 \angle 0^{\circ}}{22.36 \angle 26.57^{\circ}} = 21.47 \angle (-26.57^{\circ}) \; A $$
In the previous page we learned that the total average/real power for a balanced 3-phase circuit can be defined as: $$ P = 3V_pI_p \cos(\theta) $$ where: $$ I_p = magnitude \; of \; phase \; current $$ $$ \theta = angle \; of \; load \; impedance = angle \; between $$ $$ \qquad phase \; voltage \; and \; phase \; current $$ We now use this information to calculate the total average power of the delta-connected load as:
$$ P_{\Delta} = 3(480)(21.47)\cos(26.57^{\circ}) $$
$$ P_{\Delta} = 27.7 \; kW $$
B) The load is Wye-connected:
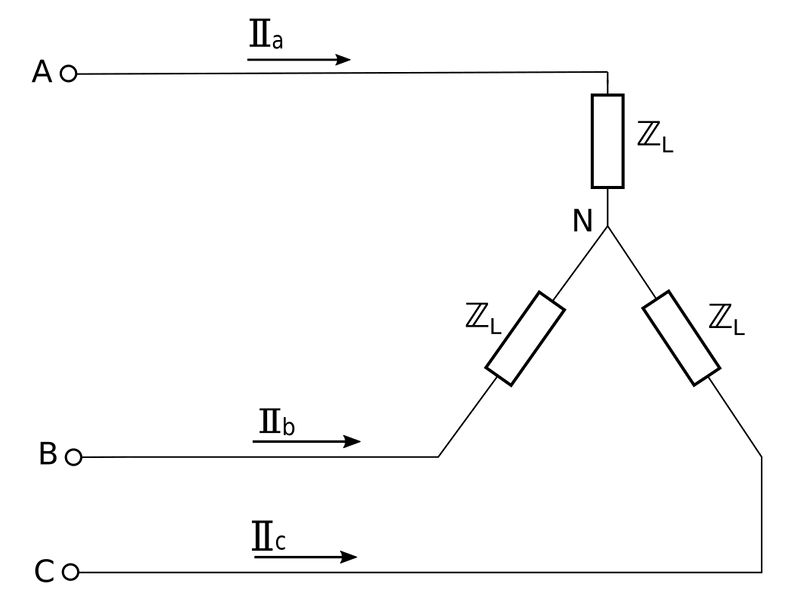
When we discussed balanced Y-Y systems, we learned that the phase voltage in terms of line voltage can be defined as: $$ V_p = \frac{V_L}{\sqrt{3}} $$ This means that for our Y-connected load we obtain the following voltage for phase "AN" (assuming positive sequence): $$ V_{AN} = \frac{480}{\sqrt{3}} = 277.1 \; V $$ By using Ohm's Law, we can determine the line current of phase "a": $$ \mathbb{I}_a = \frac{V_{AN}}{\mathbb{Z}_L} = \frac{277.1\angle 0^{\circ}}{22.36 \angle 26.57^{\circ}} $$ $$ \mathbb{I}_a = 12.39 \angle (-26.57^{\circ}) \; A $$ ...which means that the magnitude of this line current is: $$ I_a = 12.39 \; A $$
In the previous page we learned that the total average/real power for a balanced 3-phase circuit can also be defined as: $$ P = \sqrt{3} \; V_L I_L \cos(\theta) $$
We can now calculate the total average power of our Y-connected load as: $$ P_Y = \sqrt{3} \; (480)(12.39)\cos(26.57^{\circ}) $$
$$ P_Y = 9.21 \; kW $$
We now have the two values asked of us:
$$ P_{\Delta} = 27.7 \; kW $$ $$ P_Y = 9.21 \; kW $$
