Scale the low-pass filter so that the corner frequency increases from 1 rad/sec to 200 rad/sec using a 1 microfarad capacitor.
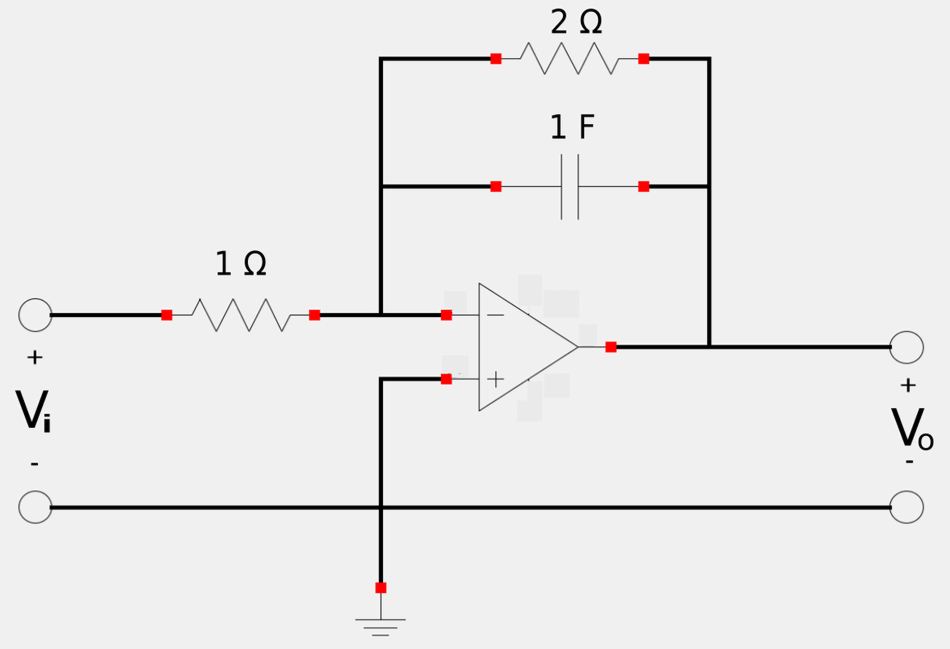
We are given the following information: $$ \omega ' = 200 \frac{rad}{s} \;,\;\;\; \omega = 1 \frac{rad}{s} $$ Since both the magnitude (impedance) and the frequency response of the circuit will be modified, we proceed to use equations #6 to calculate the frequency factor: $$ \omega ' = K_f\omega $$
$$ K_f = \frac{\omega '}{\omega} = \frac{200}{1} = 200 $$
Additionally, we are given the following information: $$ C' = 1 \mu F \;,\;\;\; C = 1F $$ We again use equations #6 to calculate the magnitude factor: $$ C' = \Big( \frac{1}{K_mK_f} \Big)C $$ $$ K_m = \Big( \frac{1}{K_f} \Big) \Big( \frac{C}{C'} \Big) $$ $$ \quad\;\; = \Big( \frac{1}{200} \Big) \Big( \frac{1}{1\times 10^{-6}} \Big) $$
$$ K_m = 5000 $$
We now use equations #6 to determine the remaining post-scaled values to the two resistors: $$ R'_1 = K_mR_1 $$ $$ \;\;\;\; = 5000(1) $$
$$ R'_1 = 5 k\Omega $$
$$ R'_2 = K_mR_2 $$ $$ \;\;\;\; = 5000(2) $$
$$ R'_2 = 10 k\Omega $$
The newly scaled circuit will look like the following:
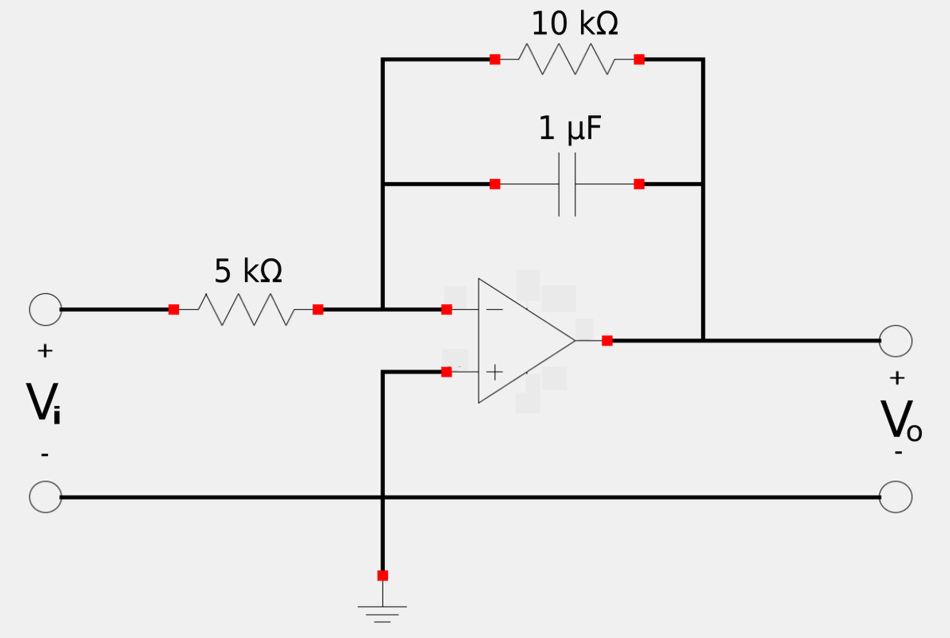
The resulting corner frequency would be 200 rad\s. Converting to hertz would give us: $$ \omega'_o = 200 \frac{rad}{s} = 2\pi f'_o $$
$$ f'_o = \frac{200}{2\pi} = 31.8 Hz $$
