Recall figure #1 from the previous page:
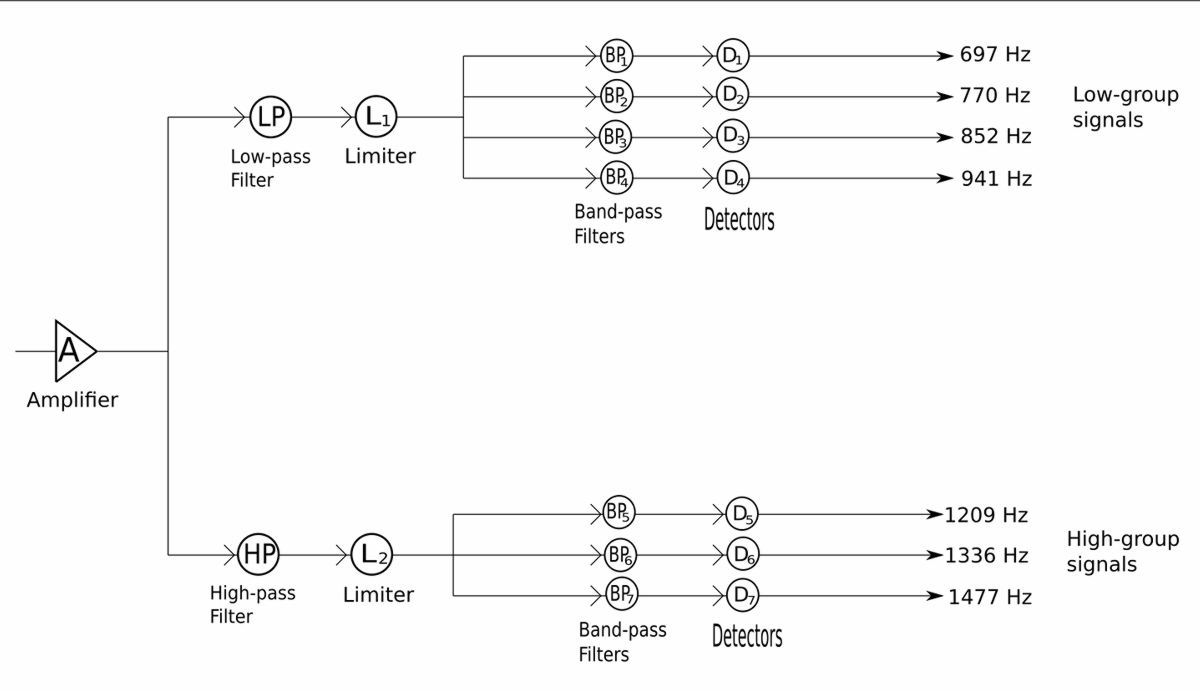
The band-pass filters in touch-tone phone detection schemes use series RLC circuits with 600Ω resistors.
Using figure #1, design the band-pass filter BP6 (band-pass filter #6).
From the block diagram we can see that BP6 must pass frequencies ranging from 1209 Hz to 1477 Hz with a center frequency of 1336 Hz. In the passive filters section we derived the band-pass filter formulas that will be used in this example problem. You will notice that these formulas require the frequencies to be angular frequencies (in terms of radians per second) and not in terms of Hertz. Therefore we convert our corner frequencies as follows:
$$ \omega_1 = 2\pi f_1 = 2\pi(1209) $$
$$ \omega_1 = 2418\pi \; \frac{rad}{s} $$
$$ \omega_2 = 2\pi f_2 = 2\pi(1477) $$
$$ \omega_2 = 2954\pi \; \frac{rad}{s} $$
...and for our center frequency we have:
$$ \omega_o = 2\pi f_o = 2\pi (1336) $$ $$ \omega_o = 2672 \; \frac{rad}{s} $$
We now calculate the bandwidth (B): $$ B = \omega_2 - \omega_1 $$ $$ \;\;\; = 2954\pi - 2418\pi $$ $$ B = 536\pi \; \frac{rad}{s} $$
Determine inductor value:
Using our band-pass filter formulas, recall that: $$ B = \frac{R}{L} $$ By rearranging terms, we determine our inductor value to be; $$ L = \frac{R}{B} = \frac{600}{536\pi} $$
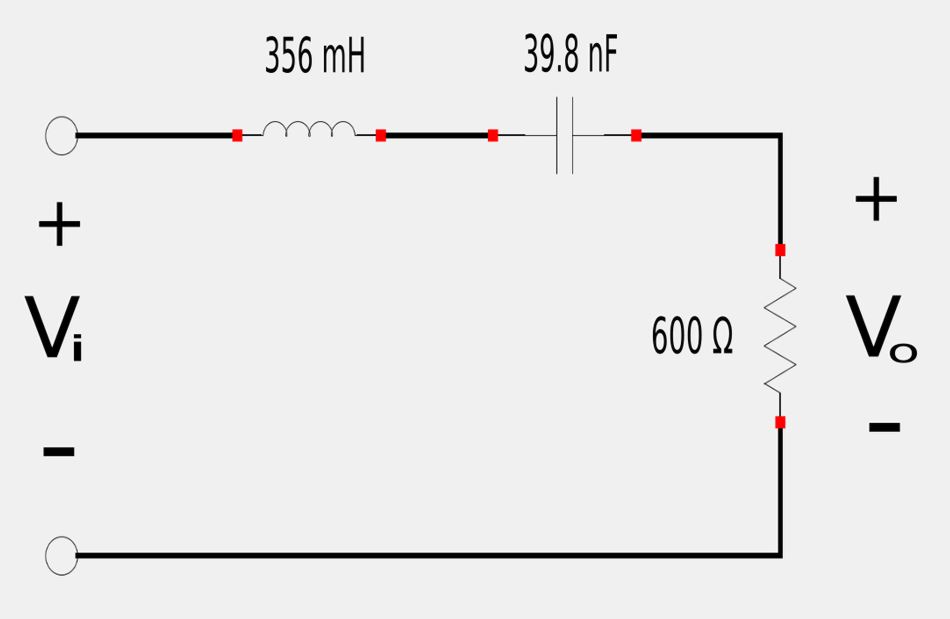
$$ L = 356.3 \; mH $$
Determine capacitor value:
Using our band-pass filter formulas, recall that: $$ \omega_o = \frac{1}{\sqrt{LC}} $$ Rearrange the terms to determine "C": $$ \sqrt{LC} = \frac{1}{\omega_o} $$ $$ C = \frac{1}{\omega_o^2 L} = \frac{1}{(2672\pi)^2(356.3\times 10^{-3})} $$
$$ C = 39.83\;nF $$
Band-pass filter #6 (BP6) will resemble the following: