For the following circuit:
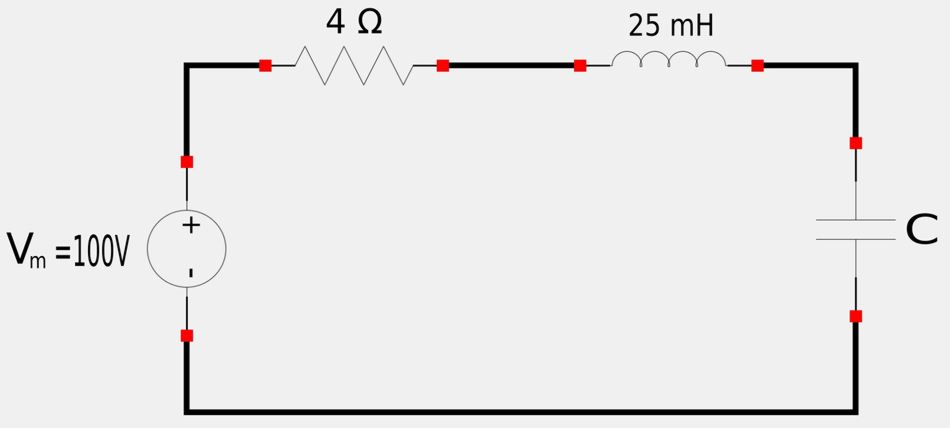
- A) Determine the capacitor value needed to achieve a quality factor of 50.
- B) Determine the 1/2 power frequencies and bandwith.
- C) Calculate the average power dissipated at resonance and at 1/2 power frequencies.
A) Determine value of C to get Q=50
First determine the resonant frequency:
In the previous page we learned that one of the expressions for the Quality Factor is: $$ Q = \frac{\omega_o L}{R} $$ Therefore: $$ \omega_o = \frac{QR}{L} = \frac{50(4)}{25 \times 10^{-3}} $$ $$ \omega_o = 8 \; kHz $$
Now calculate "C":
We also know that: $$ Q = \frac{1}{\omega_o C R} $$ Therefore: $$ C = \frac{1}{\omega_oQR} = \frac{1}{8000(50)(4)} $$
$$ C = 625 \; nF $$
B) Determine the 1/2 power frequencies and bandwith.
Calculate Bandwith (B):
In the previous page, we learned that one of the expressions for the Bandwith is: $$ B = \frac{R}{L} $$ Therefore, for our circuit: $$ B = \frac{4}{25 \times 10^{-3}} $$
$$ B = 160 \frac{rad}{s} $$
Calculate 1/2 power frequency (w2):
In the previous page, we learned that the expressions for half-power frequencies are: $$ \omega_1 = -\frac{R}{2L} + \sqrt{\Big( \frac{R}{2L} \Big)^2 + \frac{1}{LC}} $$ $$ \omega_2 = \frac{R}{2L} + \sqrt{\Big( \frac{R}{2L} \Big)^2 + \frac{1}{LC}} $$ We also just determined that: $$ C = 625 \; nF $$ Therefore:
$$ \omega_2 = \frac{4}{2(25 \times 10^{-3})} + \sqrt{\Big[ \frac{4}{2(25 \times 10^{-3})} \Big]^2 + \frac{1}{(25 \times 10^{-3})(625\times 10^{-9})}} $$
$$ \omega_2 = 8080 \; \frac{rad}{s} $$
Calculate 1/2 power frequency (w1):
In the previous page, we learned that another one of the expressions for the Bandwith is: $$ B = \omega_2 - \omega_1 $$ Therefore: $$ \omega_1 = \omega_2 - B $$ $$ \omega_1 = 8080 - 160 $$
$$ \omega_1 = 7920 \; \frac{rad}{s} $$
Alternative method (high-Q circuit):
We know that any circuit with a quality factor (Q) of 10 or greater is considered a High-Q circuit. From this knowledge we can determine the 1/2 power frequencies through the following expressions: $$ \omega_1 = \omega_o - \frac{B}{2} $$ $$ \;\;\;\; = 8000 - \frac{160}{2} $$ $$ \;\;\;\; = 7920 \; \frac{rad}{s} $$ $$ \omega_2 = \omega_o + \frac{B}{2} $$ $$ \;\;\;\; = 8000 + \frac{160}{2} $$ $$ \;\;\;\; = 8080 \; \frac{rad}{s} $$ As you can see, we get the same results as with the first method.
C) Calculate the average power dissipated at resonance and at 1/2 power frequencies
Power at resonant frequency:
One of the 4 characteristics of the resonance frequency is that the input impedance is purely resistive: $$ \mathbb{Z} = R $$ Therefore, the current magnitude can be defined as: $$ I = \frac{V}{R} $$ ...and for our circuit we have: $$ I = \frac{100}{4} = 25\;A $$ We also know that at the resonant frequency, average power can be defined as: $$ P_{\omega_o} = \frac{1}{2} V_m I_m $$ ...so for our circuit we have" $$ P_{\omega_o} = \frac{1}{2} (100)(25) $$
$$ P_{\omega_o} = 1250\;W $$
Power at 1/2 power frequencies:
Since maximum power dissipation occurs at resonance, the power at 1/2 power frequencies is equal to half of this amount: $$ P_{\omega_1} = P_{\omega_2} = \frac{1}{2}(1250) $$ $$ P_{\omega_1} = P_{\omega_2} = 625\;W $$ We could also determine this from our known expression for average power at 1/2 power frequencies: $$ p_{\omega1} = p_{\omega2} = \frac{V_m^2}{4R}$$ For our circuit, this means that: $$ p_{\omega1} = p_{\omega2} = \frac{100^2}{4(4)} $$
$$ p_{\omega1} = p_{\omega2} = 625\;W $$
