For the following circuit determine the equivalent impedance and use it to determine i(t) Let omega=10 rad/s:

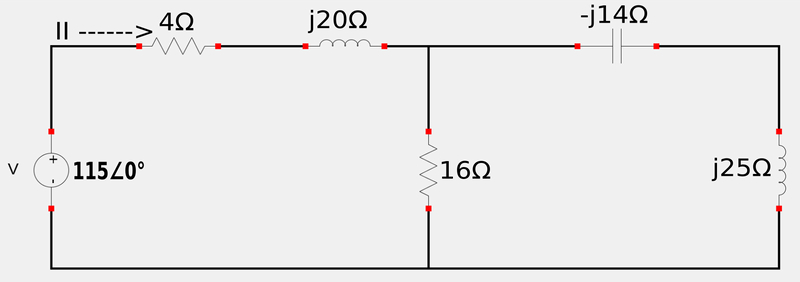
Note that voltage and current are given in phasor notation and that the impedances of the circuit elements have already been provided. Angular frequency has also been given as 10 radians per second. We begin by redrawing the circuit in a similar manner that would be used to find the equivalent resistance of a circuit. Recognize that the 4 ohm resistor and the j20 ohm inductor are in series. Additionally, the -j14 ohm capacitor and the j25 ohm inductor are also in series. The circuit now resembles the following schematic. (Note that we have now used resistor symbols to denote individual impedances.)

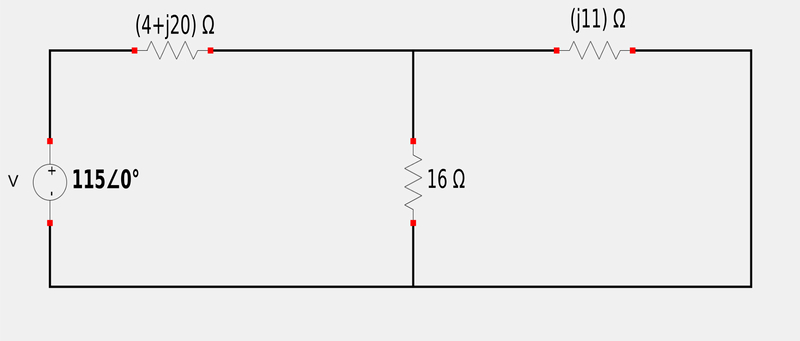
Now we examine the j11 ohm and 16 ohm impedances that are in parallel. Parallel impedances follow the same rule for resistors in parallel and the equivalent impedance of these two quantities is as follows: $$ \mathbb{Z}_{eq2} = \frac{1}{\frac{1}{j11}+\frac{1}{16}} $$ Recall that 1/j = -j $$ = \frac{1}{0.0625-j\frac{1}{11}} \qquad(expression \; 1)$$

The denominator represents a complex number with a magnitude of: $$ r = \sqrt{0.0625^2+ \Big( \frac{-1}{11} \Big)^2} $$ $$ r = 0.1103 $$ $$ \phi_{ref} = \tan^{-1} \Big( \frac{\frac{1}{11}}{0.0625} \Big) $$ $$ \phi_{ref} = \tan^{-1} \Big( \frac{16}{11} \Big) $$ $$ \phi_{ref} = 55.49^{\circ}, lies \; in \; quadrant \; IV $$ $$ \phi = -55.49^{\circ} $$ Also, note that for the numerator in expression #1: $$ 1 = 1 \angle 0^{\circ} $$ Therefore we can rewrite the parallel impedance of the j11 ohm and 16 ohm impedance values as:

$$ (Expression \; 2):$$ $$ \mathbb{Z}_{eq2} = \frac{1 \angle 0^{\circ}}{0.1103\angle (-55.49^{\circ})} $$ Using the laws of complex numbers learned in a previous tutorial, expression #2 becomes: $$ \mathbb{Z}_{eq2} = \frac{1}{0.1103} \angle(0 - (-55.49))^{\circ} $$ $$ \mathbb{Z}_{eq2} = 9.07 \angle 55.49^{\circ} $$

Converting this to rectangular form gives us: $$ x = 9.07\cos(55.49^{\circ}) = 5.14 $$ $$ y = 9.07\sin(55.49^{\circ}) = 7.47 $$ Therefor: $$ \mathbb{Z}_{eq2} = 5.14 + j7.47 $$ Our circuit can now be redrawn as the following:

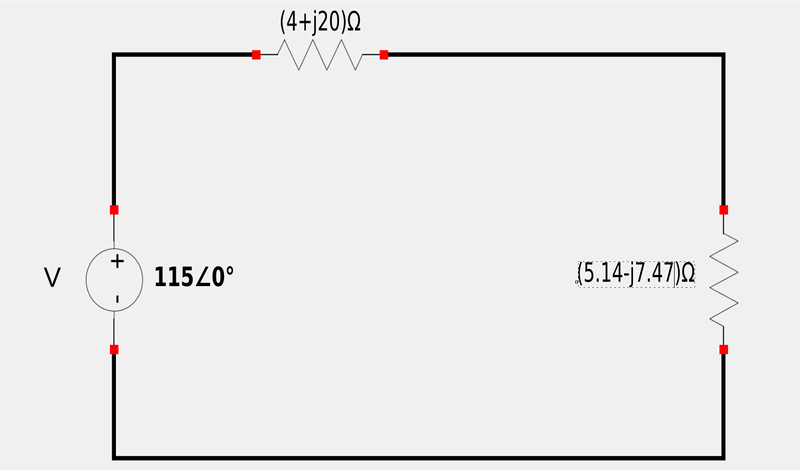
Additionally, impedances in series can be treated the same as resistors in series. Therefore: $$ \mathbb{Z}_{eq} = (4+j20) + (5.14+j7.47) $$ $$ \mathbb{Z}_{eq} = (4+5.14) + j(20+7.47) $$ ...which gives us:

The equivalent impedance of the circuit:

$$ \mathbb{Z}_{eq} = 9.14+j27.47 = 28.95 \angle 71.59^{\circ}$$

Recall Ohm's Law in the frequency domain for our circuit: $$ \mathbb{V}_s = \mathbb{I} \mathbb{Z}_{eq} $$ ...which gives us a phasor current of: $$ \mathbb{I} = \frac{\mathbb{V}_s}{\mathbb{Z}_{eq}} $$ $$ \mathbb{I} = \frac{115\angle 0^{\circ}}{28.95 \angle 71.59^{\circ}} $$ $$ \mathbb{I} = \frac{115}{28.95} \angle(0-71.59)^{\circ} $$ $$ \mathbb{I} = 3.97 \angle (-71.59)^{\circ} = 3.97e^{j(-71.59)}$$ Recall that omega = 10 and that to get i(t) we need to multiply the phasor current by e^(jwt) and take the real part of the result. Therefore: $$ i(t) = R_e \{ 3.97 e^{j(-71.59)} e^{j10t} \} $$ $$(Expression \; 3):$$ $$ i(t) = R_e \{ 3.97e^{j(10t-71.59)} \} $$

Recall Euhler's Identity: $$ e^{j\phi} = \cos\phi + j\sin\phi $$ and apply it to expression #3:

$$ i(t) = R_e \{ 3.97\cos(10t-71.59^{\circ}) + $$ $$ j3.97\sin(10t-71.59^{\circ}) \} $$ ...and when we evaluate the above expression, we get our final answer:

Current in the time-domain:

$$ i(t) = 3.97\cos(10t-71.6^{\circ}) $$

Let's take a look at another example:

Continue on to Impedance and Admittance example problem #2.