For the following circuit, determine Vo (in phasor form).

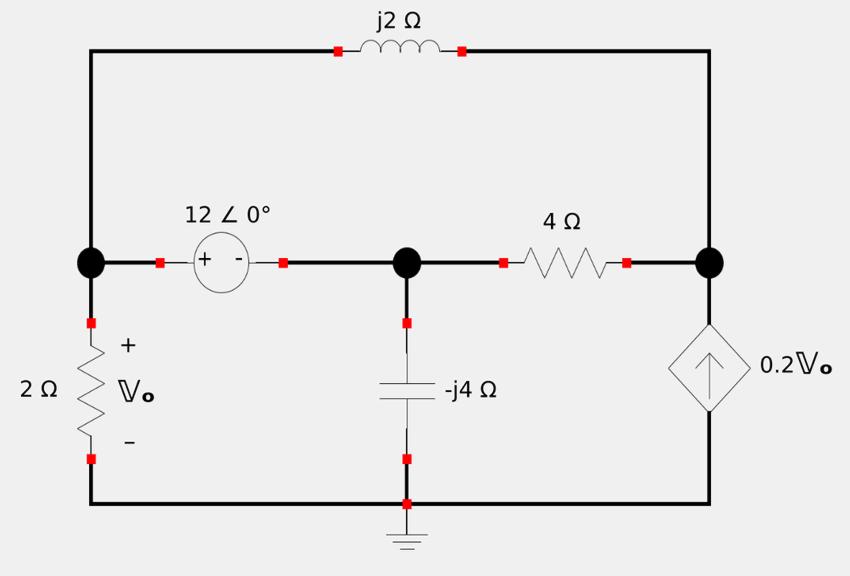
The impedances of the individual circuit elements have already been calculated for us and the circuit is already represented in the frequency domain. One thing you may notice is that we have a voltage source (independent) that lies between two non-reference nodes, meaning that the voltage source is not directly connected to our reference node depicted by the ground symbol. Just as with nodal analysis with DC circuits, this requires us to create a "super-node" that consists of the voltage source and anything that is in parallel with it (nothing is in parallel with it in this circuit). The super-node for our circuit is shown below. Phasor voltages V1 and V2 are with respect to the reference node depicted by the ground symbol:

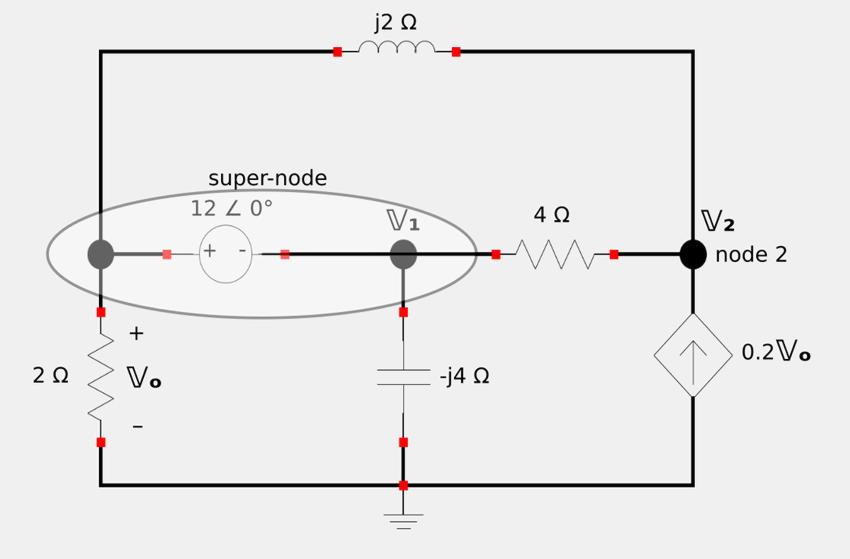
Apply KCL to the super-node:

Doing so gives us the following equation: $$ \frac{\mathbb{V}_o}{2} + \frac{\mathbb{V}_1}{-j4} + \frac{\mathbb{V}_1-\mathbb{V}_2}{4} + \frac{\mathbb{V}_o-\mathbb{V}_2}{j2} = 0 $$ We will proceed to simplify the above equation: $$ \frac{\mathbb{V}_o}{2} + \frac{j\mathbb{V}_1}{4} + \frac{\mathbb{V}_1}{4} - \frac{\mathbb{V}_2}{4} - \frac{j\mathbb{V}_o}{2} + \frac{j\mathbb{V}_2}{2} = 0 $$ $$ \mathbb{V}_o \Big[ \frac{1}{2}-\frac{j}{2} \Big] + \mathbb{V}_1 \Big[ \frac{1}{4}+\frac{j}{4} \Big] + \mathbb{V}_2 \Big[ \frac{-1}{4}+\frac{j}{2} \Big] = 0 $$ We now convert the above equation (consisting of complex numbers) from rectangular to polar form as explained in the complex numbers tutorial found here

$$ 0.7071\mathbb{V}_o \angle (-45^{\circ}) + 0.3536\mathbb{V}_1 \angle 45^{\circ} $$ $$ \qquad + 0.559\mathbb{V}_2 \angle 116.6^{\circ} = 0 \qquad,(Eqn\;1) $$

Apply KCL to node 2

Doing so gives us the following equation: $$ \frac{\mathbb{V}_2 - \mathbb{V}_1}{4} + \frac{\mathbb{V}_2 - \mathbb{V}_o}{j2} = 0.2\mathbb{V}_o $$ We again proceed to simplify the above equation: $$ \frac{-\mathbb{V}_o}{j2} - \frac{\mathbb{V}_1}{4} + \frac{\mathbb{V}_2}{4} + \frac{\mathbb{V}_2}{j2} - 0.2\mathbb{V}_o = 0 $$ $$ \mathbb{V}_o \Big[ -0.2+\frac{j}{2} \Big] + \mathbb{V}_1 \Big[ \frac{-1}{4} \Big] + \mathbb{V}_2 \Big[ \frac{1}{4}-\frac{j}{2} \Big] = 0 $$ ...and once again we convert the complex numbers from rectangular to polar form to get the following:

$$ 0.5385\mathbb{V}_o \angle 111.8^{\circ} - 0.25\mathbb{V}_1 \angle 0^{\circ} $$ $$ \qquad + 0.559\mathbb{V}_2 \angle (-63.43^{\circ}) = 0 \qquad,(Eqn\;2) $$

Use Vo and V1 to obtain a third equation:

Up to this point we have only two equations but three unknown variables. To get a third equation we notice the nodes at V1 and Vo and how the two nodes are separated by the voltage source. Since Vo is at a higher potential than V1 we have the following equation:

$$ \mathbb{V}_o - \mathbb{V}_1 = 12 \angle 0^{\circ} \qquad(Eqn\;3) $$

Solve the system of three equations (Cramer's Rule)

Several different techniques can be used to solve our system of three equations (back-substitution, matrix row operations etc...) but here we will will use Cramer's Rule. It is not necessarily the best or fastest way to solve this particular system but it affords us the opportunity to apply the rule to a real world problem. Cramer's Rule is more useful when you come across a circuit that results in a significant number of equations which would become laborious to solve using back-substitution or matrix row operations. If you are unfamiliar with using Cramer's Rule to solve systems of equations refer to this tutorial.

Create an augmented matrix of coefficients from our system of equations:

$$ \begin{pmatrix} 0.7071 \angle (-45^{\circ})&0.3536 \angle 45^{\circ}&0.559 \angle 116.6^{\circ}&0\\ 0.5385\angle 111.8^{\circ}&-0.25 \angle 0^{\circ}&0.559 \angle (-63.43^{\circ})&0\\ 1&-1&0&12 \angle 0^{\circ}\\ \end{pmatrix} $$

Find the determinant of the non-augmented matrix of coefficients:

$$ D = \begin{vmatrix} 0.7071 \angle (-45^{\circ})&0.3536 \angle 45^{\circ}&0.559 \angle 116.6^{\circ}\\ 0.5385\angle 111.8^{\circ}&-0.25 \angle 0^{\circ}&0.559 \angle (-63.43^{\circ})\\ 1&-1&0\\ \end{vmatrix} $$ The tedious grunt work of obtaining the determinant will be left to you, but by following the Cramer's Rule tutorial and example problem you should get a determinant of:

$$ D = 0.2183 \angle (-23.65^{\circ}) $$

Create a matrix that consists of the matrix of coefficients with its 1st column replaced by the 4th column of the augmented matrix of coefficients

...and proceed to find the determinant: $$ D_{\mathbb{V}_o} = \begin{vmatrix} 0&0.3536 \angle 45^{\circ}&0.559 \angle 116.6^{\circ}\\ 0&-0.25 \angle 0^{\circ}&0.559 \angle (-63.43^{\circ})\\ 12\angle 0^{\circ}&-1&0\\ \end{vmatrix} $$ ...which will be:

$$ D_{\mathbb{V}_o} = 1.677 \angle 26.23^{\circ} $$

We don't need to proceed further since we are only looking to solve for Vo and by Cramer's Rule, Vo is $$ \mathbb{V}_o = \frac{D_{\mathbb{V}_o}}{D} = \frac{1.677 \angle 26.23^{\circ}}{0.2183 \angle (-23.65^{\circ})} $$

$$ \mathbb{V}_o = 7.682 \angle 49.88^{\circ} $$