For the following circuit, find the Thevenin equivalent circuit at terminals a-b:
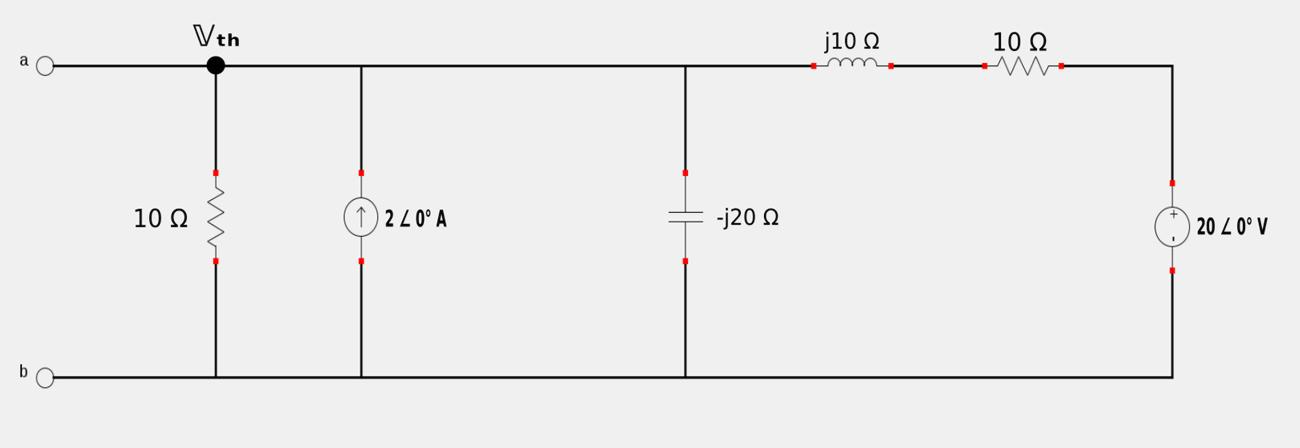
Recall the process used to determine a Thevenin equivalent circuit:
- Determine the open-circuit voltage across terminals a-b. OR:
- Determine the short-circuit current through terminals a-b. (Choose whichever is easiest for steps 1,2)
- Determine the equivalent impedance at terminals a-b when independent sources are "turned off". (Do not "turn off" dependant sources.)
- Solve for the unknown using Ohm's Law $$ \mathbb{Z}_{th} = \mathbb{Z}_n = \frac{\mathbb{V}_{th}}{\mathbb{I}_n} $$
When considering steps one and two we will choose option one (open-circuit voltage at terminals a-b).
Step 1: Get the open-circuit voltage at terminals a-b:
We start by applying Kirchhoff's Current Law (KCL) at terminal/node "a": $$ \frac{\mathbb{V}_{th}}{10} + \frac{j\mathbb{V}_{th}}{20} + \frac{\mathbb{V}_{th}-20}{10+j10} = 2 $$ Multiply the third term in the above equation by its complex conjugate: $$ \frac{\mathbb{V}_{th}}{10} + \frac{j\mathbb{V}_{th}}{20} + \frac{\mathbb{V}_{th}-20}{10+j10} \Big( \frac{10-j10}{10-j10} \Big) = 2 $$ $$ \frac{\mathbb{V}_{th}}{10} + \frac{j\mathbb{V}_{th}}{20} + \frac{10\mathbb{V}_{th}-j10\mathbb{V}_{th}-200+j200}{200} = 2 $$ $$ \frac{\mathbb{V}_{th}}{10} + \frac{j\mathbb{V}_{th}}{20} + \frac{\mathbb{V}_{th}}{20} - \frac{j\mathbb{V}_{th}}{20} - 1 + j = 2 $$ Multiply the above expression by 20 $$ 2\mathbb{V}_{th} + j\mathbb{V}_{th} + \mathbb{V}_{th} - j\mathbb{V}_{th} -20 + j20 = 40 $$ $$ 3\mathbb{V}_{th} + j20 = 60 $$ $$ 3\mathbb{V}_{th} = 60 - j20 = 63.25 \angle (-18.43^{\circ}) $$
$$\mathbb{V}_{th} = 21.08 \angle (-18.43^{\circ})$$
Step 2: Get the equivalent impedance at terminals a-b (with independent sources "turned off"):
With the independent sources "turned off" we have the following circuit with labeled impedances:
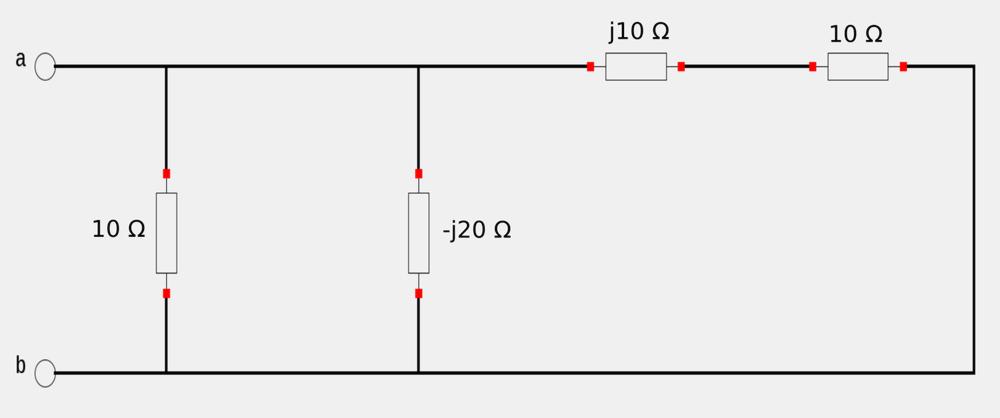
The equivalent impedance can be summarized by the following parallel/series impedance combination: $$ \mathbb{Z}_{th} = (10) \;||\; (-j20) \;||\; (10+j10) $$ $$ = \frac{1}{\frac{1}{10}+\frac{j}{20}} \;\Big|\Big|\; (10+j10) $$ We now multiply the complex term in the denominator by its complex conjugate: $$ = \frac{1(\frac{1}{10}-\frac{j}{20})}{\frac{1}{10}+\frac{j}{20}(\frac{1}{10}-\frac{j}{20})} \;\Big|\Big|\; (10+j10) $$ $$ \mathbb{Z}_{th} = \frac{0.1-j0.05}{0.0125} \Big|\Big| 10+j10 $$ $$ = 8-j4 || 10+j10 $$ Applying the rule of impedances in parallel and multiplying by the complex conjugates at the same time gives us: $$ \mathbb{Z}_{th} = \frac{1}{\frac{1}{8-j4}\frac{8+j4}{8+j4} + \frac{1}{10+j10}\frac{10-j10}{10-j10}} $$ $$ = \frac{1}{\frac{8+j4}{80} + \frac{10-j10}{200}} $$ $$ = \frac{1}{0.1+j0.05+0.05-j0.05} $$
$$ \mathbb{Z}_{th} = 6.667 \; \Omega $$
Now that we have determined the Thevenin voltage and impedance, our Thevenin equivalent circuit will look like the following:
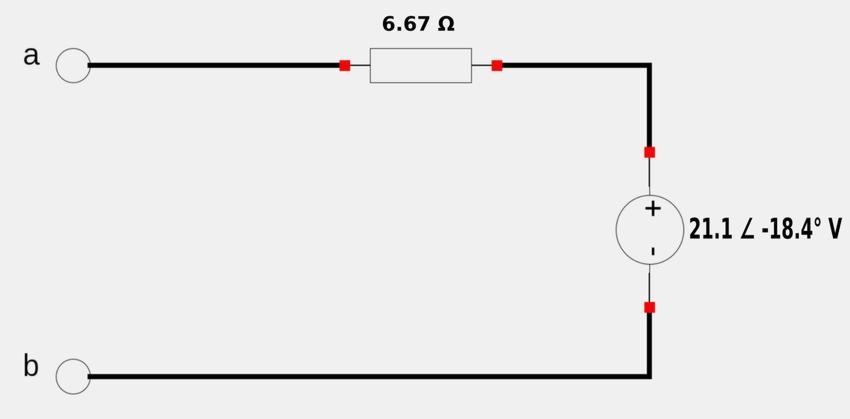
Let's take a look at another example problem.
Continue on to Thevenin and Norton circuits example 2
