For the following circuit, find the Thevenin equivalent circuit at terminals a-b:
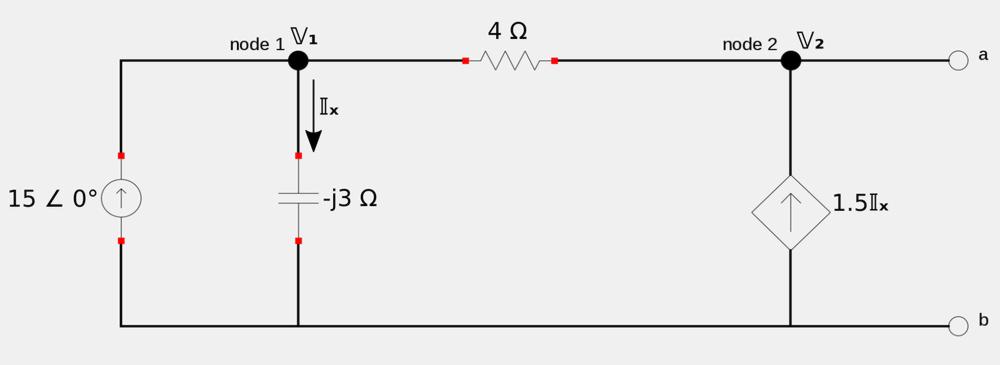
(Note: The independent current source is in units of amps, A)
Recall the process used to determine a Thevenin equivalent circuit:
- Determine the open-circuit voltage across terminals a-b. OR:
- Determine the short-circuit current through terminals a-b. (Choose whichever is easiest for steps 1,2)
- Determine the equivalent impedance at terminals a-b when independent sources are "turned off". (Do not "turn off" dependant sources.)
- Solve for the unknown using Ohm's Law $$ \mathbb{Z}_{th} = \mathbb{Z}_n = \frac{\mathbb{V}_{th}}{\mathbb{I}_n} $$
Step 1: Get the open-circuit voltage at terminals a-b:
Apply Kirchhoff's Current Law (KCL) at node 2:
$$ \frac{\mathbb{V}_{th}-\mathbb{V}_1}{4} = 1.5\mathbb{I}_x $$
However, note that: $$ \mathbb{I}_x = \frac{\mathbb{V}_1}{-j3} = \frac{j\mathbb{V}_1}{3} $$ which allows us to rewrite our original equation as:
$$ \frac{\mathbb{V}_{th}-\mathbb{V}_1}{4} = \Big( \frac{3}{2} \Big) \Big( \frac{1}{3} \Big) j\mathbb{V}_1 $$ $$ \frac{\mathbb{V}_{th}-\mathbb{V}_1}{4} = j0.5\mathbb{V}_1 $$ $$ \frac{\mathbb{V}_{th}}{4} - \frac{\mathbb{V}_1}{4} - j0.5\mathbb{V}_1 = 0 $$ We now multiply the above equation by (-4) and get: $$ \mathbb{V}_1 + j2\mathbb{V}_1 - \mathbb{V}_{th} = 0 $$ $$ \mathbb{V}_1(1+j2) - \mathbb{V}_{th} = 0 $$ ...and if we convert the above equation to polar form we get:
$$ 2.236\mathbb{V}_1 \angle 63.43^{\circ} - \mathbb{V}_{th} \angle 0^{\circ} = 0 \;\;\; ,(Eqn \; 1) $$
Apply Kirchhoff's Current Law (KCL) at node 1:
$$ \frac{j\mathbb{V}_1}{3} + \frac{\mathbb{V}_1-\mathbb{V}_{th}}{4} = 15 $$ $$ \frac{j\mathbb{V}_1}{3} + \frac{\mathbb{V}_1}{4} - \frac{\mathbb{V}_{th}}{4} = 15 $$ Now multiply the above equation by 12 and get: $$ j4\mathbb{V}_1 + 3\mathbb{V}_1 - 3\mathbb{V}_{th} = 180 $$ $$ \mathbb{V}_1(3+j4) - 3\mathbb{V}_{th} = 180 $$ ...and if we convert the above equation to polar form we get:
$$ 5\mathbb{V}_1 \angle 53.13^{\circ} - 3\mathbb{V}_{th} \angle 0^{\circ} = 180 \;\;\; ,(Eqn \; 2) $$
If we use a matrix to represent our system of two equations (Equations 1 and 2) we have: $$ \begin{pmatrix} 2.236 \angle 63.43^{\circ}&-1 &0\\ 5\angle 53.13^{\circ}&- 3 &180\\ \end{pmatrix} $$ If we solve this system of equations using Cramer's Rule (refer to previous examples of doing this in the AC circuits sections), we get a Thevenin voltage value of:
$$ \mathbb{V}_{th} = 201.3 \angle 153.4^{\circ} = -180+j90.13 $$
Step 2: Determine Thevenin equivalent impedance
We being to do this by "turning off" the independent current source. Since this circuit has a dependent source (which can't be turned off), we refer to the introduction to Thevenin and Norton circuits page and recall that the way to proceed is to apply a "dummy" current source of 1A at terminals a-b. This current source will be referred to as IIo. After applying the dummy source, we determine the resulting voltage at terminals a-b (referred to as Vo) and then find the Thevenin impedance by: $$ \mathbb{Z}_{th} = \frac{\mathbb{V}_o}{\mathbb{I}_o} $$ The redrawn circuit used to accomplish all of the above will look like the following:
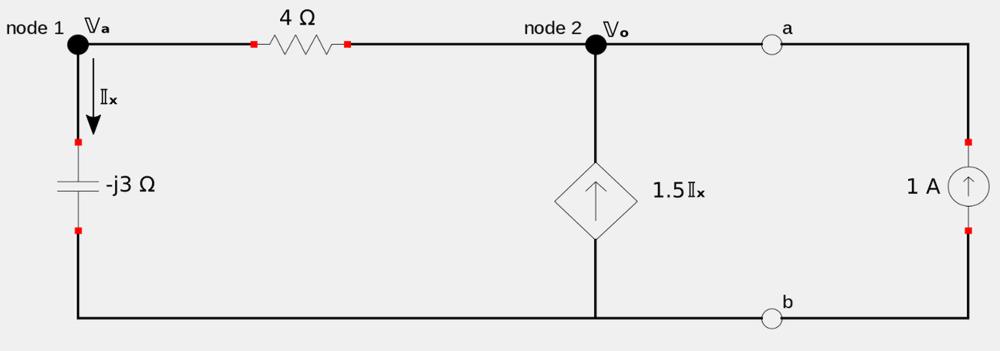
Apply KCL at node 2:
$$ \frac{\mathbb{V}_o - \mathbb{V}_a}{4} = 1 + 1.5\mathbb{I}_x $$
However, note that: $$ \mathbb{I}_x = \frac{\mathbb{V}_a}{-j3} = \frac{j\mathbb{V}_a}{3} $$ This allows us to rewrite the original equation as:
$$ \frac{\mathbb{V}_o - \mathbb{V}_a}{4} = 1 + 1.5\Big( \frac{j\mathbb{V}_a}{3} \Big) $$ $$ \frac{\mathbb{V}_o}{4} - \frac{\mathbb{V}_a}{4} - \frac{j\mathbb{V}_a}{2} = 1 $$ Mulitply the above equation by (-4) and get: $$ -\mathbb{V}_o + \mathbb{V}_a +j2\mathbb{V}_a = -4 $$ $$ \mathbb{V}_a(1+j2) - \mathbb{V}_o = -4 $$ Lastly, conver the above equation to polar form:
$$ 2.236\mathbb{V}_a \angle 63.43^{\circ} - \mathbb{V}_o \angle 0^{\circ} = -4 \;\;\; ,(Eqn \; 3)$$
Apply KCL at node 1:
$$ \frac{j\mathbb{V}_a}{3} + \frac{\mathbb{V}_a - \mathbb{V}_o}{4} = 0 $$ Multiplying through by 12: $$ j4\mathbb{V}_a + 3\mathbb{V}_a - 3\mathbb{V}_o = 0 $$ $$ \mathbb{V}_a(3+j4) - 3\mathbb{V}_o = 0 $$ Once again, convert the above expression to polar form:
$$ 5\mathbb{V}_a \angle 53.13^{\circ} - 3\mathbb{V}_o \angle 0^{\circ} = 0 \;\;\; ,(Eqn \; 4) $$
Solving equations 3 and 4 (by whatever method you choose) will give you: $$ \mathbb{V}_o = 10 \angle 143.1^{\circ} $$
Recall that: $$ \mathbb{Z}_{th} = \frac{\mathbb{V}_o}{\mathbb{I}_o} = \frac{10 \angle 143.1^{\circ}}{1}$$
$$ \mathbb{Z}_{th} = 10 \angle 143.1^{\circ} \; \Omega = -8.003+j6 \; \Omega $$
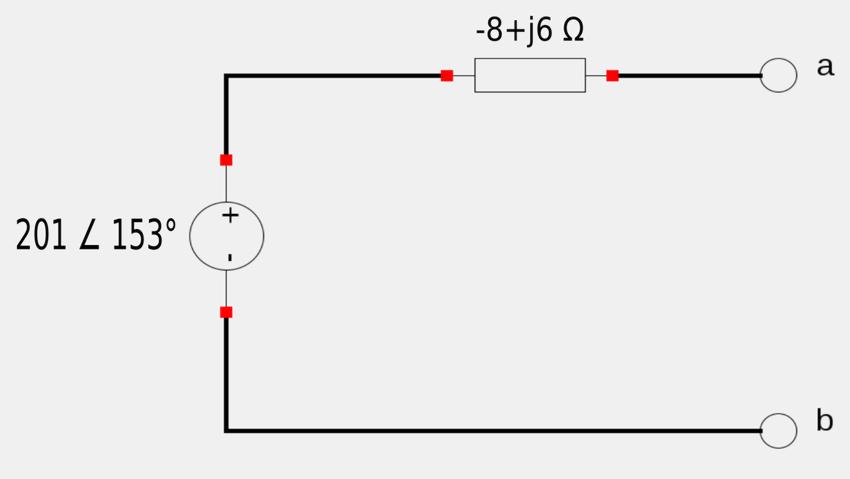
We now have our Thevenin equivalent circuit (shown below):