For the following circuit, determine the type of filter and calculate the corner frequency.
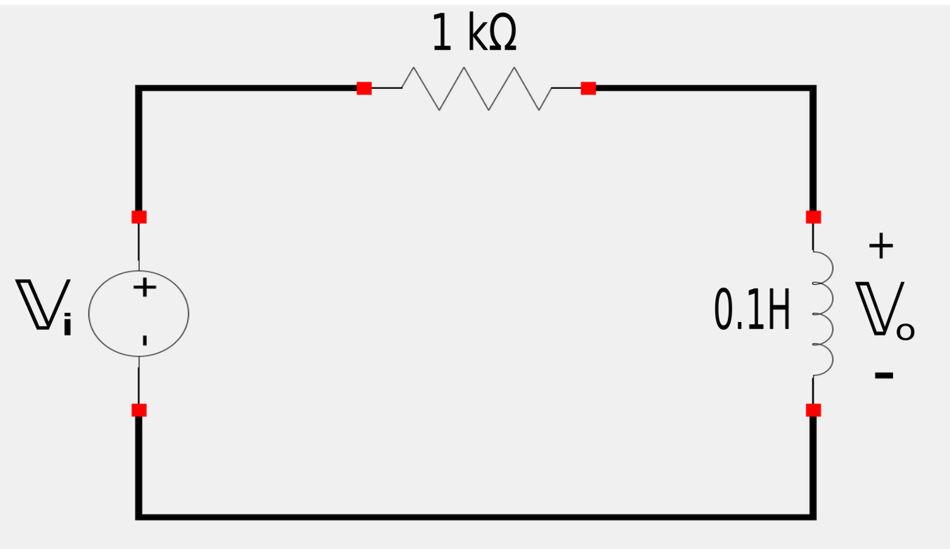
1) Determine the transfer function
By the principle of voltage division we have: $$ \mathbb{V}_o = \frac{\mathbb{Z}_L}{R+\mathbb{Z}_L} \mathbb{V}_i $$ $$ \frac{\mathbb{V}_o}{\mathbb{V}_i} = \frac{\mathbb{Z}_L}{R+\mathbb{Z}_L} = \mathbb{H}(s) $$ Recalling that: $$ \mathbb{Z}_L = j\omega L = j\omega 0.1 $$ ...and that: $$ j\omega = s $$ ...we have: $$ \mathbb{H}(s) = \frac{0.1s}{1000+0.1s} $$ Dividing the above expression by 1000 gives us our transfer function:
$$ \mathbb{H}(s) = \frac{(100\times 10^{-6})s}{1+(100\times 10^{-6})s} \qquad,(Eqn\;1) $$
2) Determine the magnitude of the transfer function
Begin by replacing "s" with "jw" in equation #1: $$ \mathbb{H}(j\omega) = \frac{(100\times 10^{-6})j\omega}{1+(100\times 10^{-6})j\omega} $$ The magnitude is as follows:
$$ |\mathbb{H}(j\omega)| = \frac{(100\times 10^{-6})\omega}{\sqrt{1+(10\times 10^{-9})\omega^2}} \qquad,(Eqn\;2) $$
Determine the magnitude at w=0 and w=infinity
Using equation #2 we get: $$ |\mathbb{H}(0)| = \frac{0}{1} = 0 $$ Additionally we have: $$ |\mathbb{H}(\infty)| = \frac{\infty}{\infty} $$ Since the above expression is indefinite we proceed as follows: Square the numerator and denominator of equation #2 and get the following: $$ |\mathbb{H}(j\omega)| = \frac{(10\times 10^{-9})\omega^2}{1+(10\times 10^{-9})\omega^2} $$ Now we can divide the numerator and denominator by w^2 and obtain the magnitude of the transfer function in the following form: $$ |\mathbb{H}(j\omega)| = \frac{10\times 10^{-9}}{\frac{1}{\omega^2} + (10\times 10^{-9}) } \qquad, (Eqn\;3) $$ Using equation #3 we can now determine that: $$ |\mathbb{H}(\infty)| = \frac{10\times 10^{-9}}{0+10\times 10^{-9}} = 1 $$
Having just determined that: $$ |\mathbb{H}(0)| = 0 $$ and: $$ |\mathbb{H}(\infty)| = 1 $$ We can surmise that this filter blocks low frequencies and passes high frequencies making the circuit a high-pass filter.
Determine the corner frequency
In the previous page we learned that the cutoff/corner frequency for a high-pass filter can be found by setting the magnitude equal to 1/sqrt(2). Therefore we use equation #2 and get the following expression: $$ \frac{(100\times 10^{-6})\omega}{\sqrt{1+(10\times 10^{-9})\omega^2}} = \frac{1}{\sqrt{2}} $$ We now proceed to solve for omega in order to determine the corner frequency. Begin by squaring both sides of the above expression: $$ \frac{(10\times 10^{-9})\omega^2}{1+(10\times 10^{-9})\omega^2} = \frac{1}{2} $$ $$ 20\times 10^{-9} \omega^2 = 1+(10\times 10^{-9})\omega^2 $$ $$ (10\times 10^{-9})\omega^2 = 1 $$ $$ \omega^2 = 100\times 10^6 $$
Corner frequency
$$ \omega = (10\times 10^3) \; \frac{rad}{s} = \omega_c $$
Continue on to passive filter example problem #2...
