Calculate the Resonant Frequency for the following circuit:
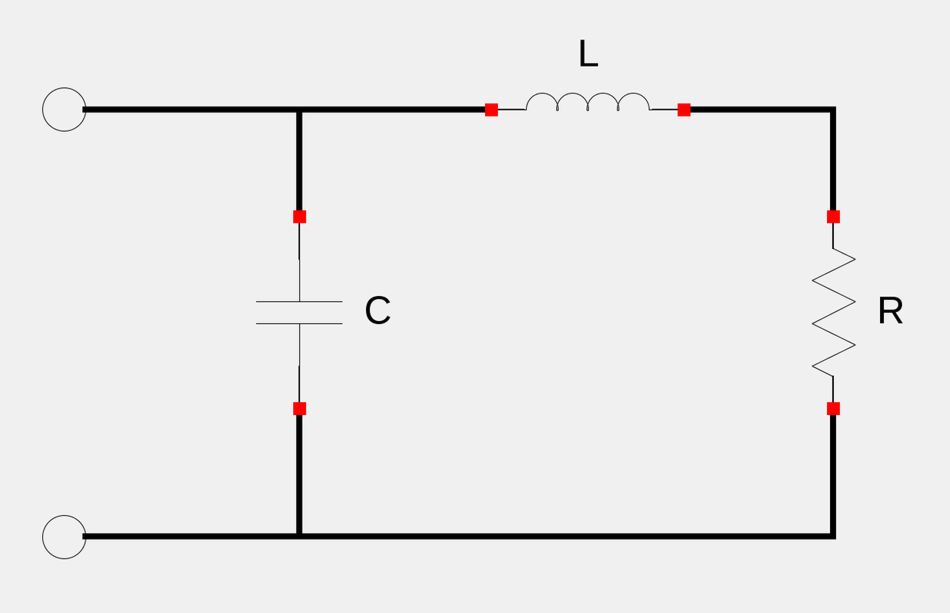
1) Determine the input admittance:
The admittance of the capacitor is defined as: $$ \mathbb{Y}_C = j\omega C $$ The admittance of the inductor is defined as: $$ \mathbb{Y}_L = \frac{1}{j\omega L} = \frac{-j}{\omega L} $$ The admittance of the resistor is defined as: $$ \mathbb{Y}_R = \frac{1}{R} $$ Recall that the rules for admittances in series and parallel are the inverse of the rules for impedances in series and parallel. Therefore, we can now define the input admittance of the circuit as: $$ \mathbb{Y}_{in} = \mathbb{Y}_C + \frac{1}{\frac{1}{\mathbb{Y}_L} + \frac{1}{\mathbb{Y}_R}} $$ $$ \quad \;\; = \mathbb{Y}_C + \frac{1}{\frac{\mathbb{Y}_R+\mathbb{Y}_L}{\mathbb{Y}_L\mathbb{Y}_R}} $$ $$ \mathbb{Y}_{in} = \mathbb{Y}_C + \frac{\mathbb{Y}_L\mathbb{Y}_R}{\mathbb{Y}_R+\mathbb{Y}_L} $$ Substituting the expressions for the individual admittances of the capacitor, inductor and resistor gives us: $$ \mathbb{Y}_{in} = j\omega C + \frac{(\frac{-j}{\omega L})(\frac{1}{R})}{\frac{1}{R}-\frac{j}{\omega L}} $$ We now proceed to multiply the second term by its complex conjugate in order to remove the imaginary part from the denominator: $$ \quad \;\; = j\omega C + \frac{(\frac{-j}{\omega L})(\frac{1}{R})}{\frac{1}{R}-\frac{j}{\omega L}} \Big( \frac{\frac{1}{R}+\frac{j}{\omega L}}{\frac{1}{R}+\frac{j}{\omega L}} \Big) $$ $$ \quad \;\; = j\omega C + \frac{(\frac{-j}{\omega LR})(\frac{1}{R})+(\frac{-j}{\omega LR})(\frac{j}{\omega L})}{\frac{1}{R^2}+\frac{1}{\omega^2 L^2}} $$ $$ \quad \;\; = j\omega C + \frac{\frac{-j}{\omega LR^2}+\frac{1}{\omega^2 L^2R}}{\frac{1}{R^2}+\frac{1}{\omega^2L^2}} $$ $$ \quad \;\; = j\omega C + \frac{\frac{-j}{\omega LR^2}+\frac{1}{\omega^2L^2R}}{\frac{\omega^2L^2+R^2}{R^2\omega^2L^2}} $$ $$ \quad \;\; = j\omega C + \Big( \frac{-j}{\omega LR^2}+\frac{1}{\omega^2L^2R} \Big) \Big( \frac{R^2\omega^2L^2}{\omega^2L^2+R^2} \Big) $$ $$ \quad \;\; = j\omega C + \Big( \frac{-jR^2\omega^2L^2}{\omega^3L^3R^2+\omega LR^4} + \frac{R^2\omega^2L^2}{\omega^4L^4R+\omega^2L^2R^3} \Big) $$
$$ \mathbb{Y}_{in} = \frac{R^2\omega^2L^2}{\omega^4L^4R+\omega^2L^2R^3} + j \Big( \omega C - \frac{R^2\omega^2L^2}{\omega^3L^3R^2+\omega LR^4} \Big) \quad, (Eqn\;1) $$
Determine the resonant frequency:
Recall that a circuit is at its resonant frequency when the admittance is purely conductive. This means that the following expression must be true: $$ I_m \{ \mathbb{Y}_{in} \} = 0 $$ Applying this knowledge to equation #1 gives us: $$ \omega C - \frac{R^2\omega^2L^2}{\omega^3L^3R^2+\omega LR^4} = 0 $$ $$ \omega C = \frac{R^2\omega^2L^2}{\omega^3L^3R^2+\omega LR^4} $$ $$ C = \frac{\omega L^2 R^2}{\omega^3L^3R^2+\omega LR^4} $$ $$ \omega L^2 R^2 = \omega^3L^3R^2C + \omega LR^4C $$ $$ \omega^3L^3R^2C + \omega LR^4C - \omega L^2 R^2 = 0 $$ $$ \omega (\omega^2L^3R^2C + LR^4C - L^2R^2) = 0 $$ $$ \omega^2L^3R^2C + LR^4C - L^2R^2 = 0 $$ $$ \omega^2 = \frac{L^2R^2-LR^4C}{L^3R^2C} $$ $$ \omega^2 = \frac{L^2R^2}{L^3R^2C} - \frac{LR^4C}{L^3R^2C} $$ $$ \omega^2 = \frac{1}{LC}-\frac{R^2}{L^2} $$
$$ \omega = \sqrt{\frac{1}{LC}-\frac{R^2}{L^2}} = \omega_o $$
Continue on to parallel resonance (example problem #3)...
