Given the following circuit:
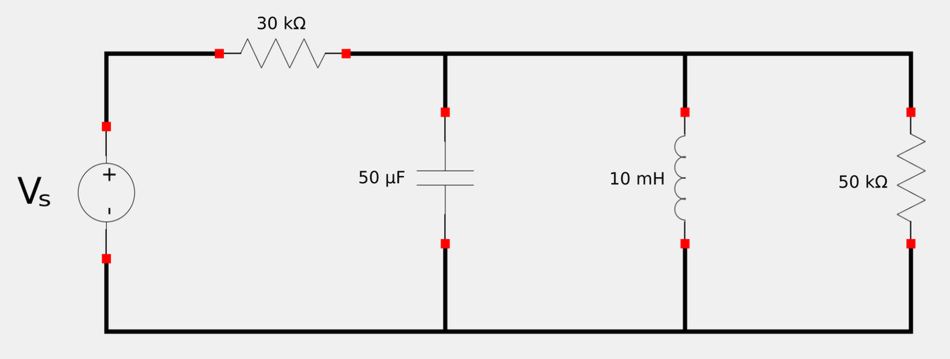
Calculate the resonant frequency, bandwidth and quality factor as seen by the voltage across the inductor.
Perform a source transformation:
We begin by replacing the voltage source in series with the 30 kOhm resistor with its Norton equivalent current source in parallel with the resistor. This source transformation is shown below:
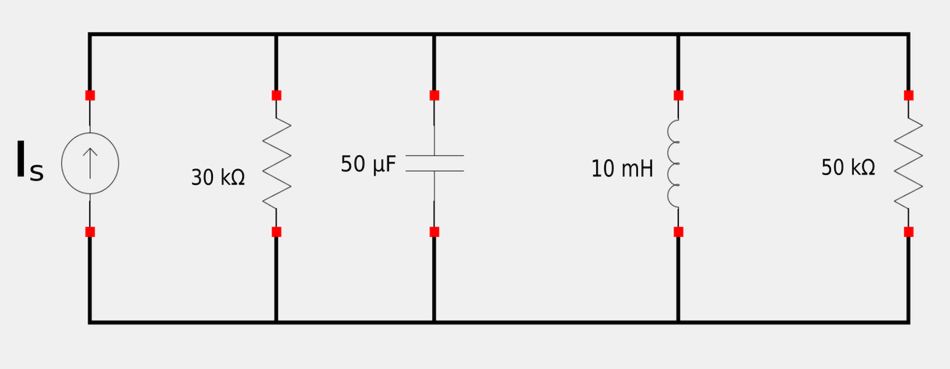
Determine the input admittance:
The equivalent resistance of our circuit is: $$ R_{eq} = \frac{1}{\frac{1}{30,000}+\frac{1}{50,000}} = 18.75\;k\Omega $$ Therefore, the admittance: of our resistors in parallel is: $$ \mathbb{Y}_R = \frac{1}{R_{eq}} = \frac{1}{18750} = 53.33 \; \mu S $$ The admittance of the capacitor is defined as: $$ \mathbb{Y}_C = j\omega C = j\omega(50\times 10^{-6}) $$ The admittance of the inductor is defined as: $$ \mathbb{Y}_L = \frac{1}{j\omega L} = \frac{-j}{\omega L} $$ $$ \mathbb{Y}_L = \frac{-j}{\omega(10\times 10^{-3})} $$ Recall that the rule for admittances in parallel is the inverse of the rule for impedances in parallel. Therefore, we can now define the input admittance of the circuit as: $$ \mathbb{Y}_{in} = \mathbb{Y}_R + \mathbb{Y}_C + \mathbb{Y}_L $$ $$ \quad \; = 53.33 \times 10^{-6} + j\omega(50\times 10^{-6}) - \frac{j}{\omega(10\times 10^{-3})} $$
$$ \mathbb{Y}_{in} = 53.33 \times 10^{-6} + j \Big[\omega(50\times 10^{-6}) - \frac{1}{\omega(10\times 10^{-3})} \Big] \quad, (Eqn\;1)$$
Calculate the resonant frequency:
Recall that a circuit is at its resonant frequency when the admittance is purely conductive. This means that the following expression must be true: $$ I_m \{ \mathbb{Y}_{in} \} = 0 $$ Applying this knowledge to equation #1 gives us: $$ \omega(50\times 10^{-6}) - \frac{1}{\omega(10\times 10^{-3})} = 0 $$ $$ \omega(50\times 10^{-6}) = \frac{1}{\omega(10\times 10^{-3})} $$ $$ \omega^2 = 2\times 10^6 $$
$$ \omega = 1414 \; \frac {rad}{s} = \omega_{o} $$
Alternatively, we could have obtained the resonant frequency via the following equation: $$ \omega_0 = \frac{1}{\sqrt{LC}} $$ $$ \quad = \frac{1}{\sqrt{(10\times 10^{-3})(50\times 10^{-6})}} $$ $$ \omega_0 = 1414 \; \frac {rad}{s} $$
Calculate the bandwidth:
In the intro to parallel resonance page, we learned that bandwidth is defined as: $$ B = \frac{1}{RC} $$ $$ B = \frac{1}{(18750)(50 \times 10^{-6})} $$
$$ B = 1.067 \frac{rad}{s} $$
Calculate the quality factor:
In the intro to parallel resonance page, we also learned that the quality factor can be defined as: $$ Q = \frac{\omega_o}{B} $$ $$ Q = \frac{1414}{1.067} $$
$$ Q = 1325 $$
