Consider the following three-phase transformer connected to a 120 kVA load:
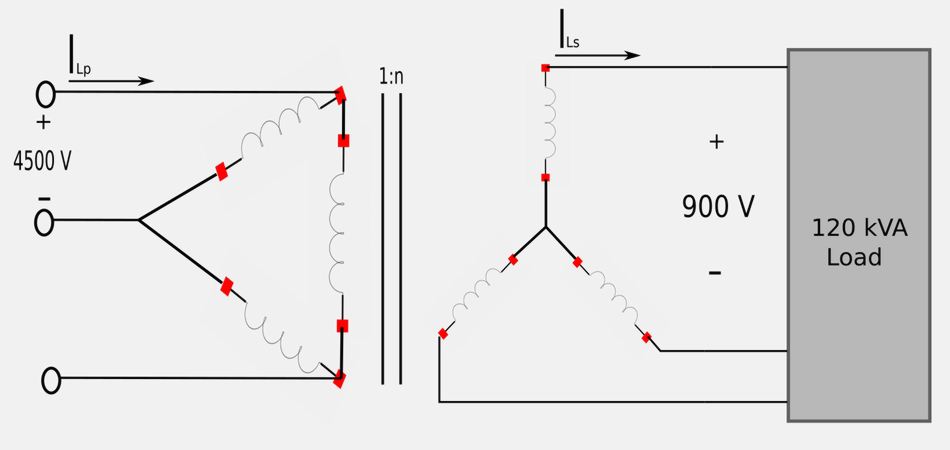
- A) Calculate the turns ration "n".
- B) Calculate the line currents for primary and secondary sides.
A) Determine the turns ratio
Recall from the intro page to 3-phase transformers, that the secondary line voltage for delta-wye configuration is defined as: $$ V_{Ls} = n\sqrt{3} V_{Lp} $$ ...where: $$ V_{Ls} = secondary \; line \; voltage $$ $$ V_{Lp} = primary \; line \; voltage $$ Therefore, the turns ratio is defined as: $$ n = \frac{V_{Ls}}{\sqrt{3}V_{Lp}} = \frac{900}{\sqrt{3}(4500)} $$
$$ n = 0.1155 $$
B) Calculate primary and secondary line currents
Secondary:
Recall that the total apparent power for the primary or secondary side of any three-phase transformer can be defined as: $$ S_T = \sqrt{3} V_L \; I_L $$ where: $$ V_L = line \; voltage $$ $$ I_L = line \; current $$ For the secondary side, we are given a load with an apparent power value of 120 kVA. Therefore we have the following expression for the apparent power of the secondary side: $$ S_{Ts} = \sqrt{3} V_{Ls} \; I_{Ls} $$ $$ I_{Ls} = \frac{S_{Ts}}{\sqrt{3} V_{Ls}} = \frac{120,000}{\sqrt{3}(900)} $$
$$ I_{Ls} = 76.98 \; A $$
Primary:
Now recall the expression for the line currents of a 3-phase delta-wye configuration: $$ I_{Ls} = \frac{I_{Lp}}{n\sqrt{3}} $$ ...where: $$ I_{Ls} = secondary \; line \; current $$ $$ I_{Lp} = primary \; line \; current $$ By rearranging the above expression we arrive at the following equation for the secondary line current: $$ I_{Lp} = n\sqrt{3} I_{Ls} = (0.1155)(\sqrt{3})(76.98)$$
$$ I_{Lp} = 15.4 \; A $$
Alternative method for determining primary line current:
Additionally, we can determine the primary line current by recognizing that power is conserved in an ideal transformer. For apparent power (S) this means that: $$ S_{Ts} = S_{Tp} = \sqrt{3} V_{Lp} \; I_{Lp} = 120,000 $$ $$ \sqrt{3} V_{Lp} \; I_{Lp} = 120,000 $$ $$ I_{Lp} = \frac{120,000}{\sqrt{3} V_{Lp}} = \frac{120,000}{(\sqrt{3}) (4500)} $$ As you can see, we get the same answer as the first method:
$$ I_{Lp} = 15.4 \; A $$
