Aside from large power distribution networks used by public utilities, you will find several real-world uses for transformers. Here we briefly mention four of them.
1) Electrical Isolation.
Many household appliances and electrical devices utilize transformers to not only step-down AC voltages, but also to electrically isolate the device from the household 120V or 240V line voltage. This is done to reduce the risk of electric shock when handling the device. Additionally, after stepping down the voltage and providing electrical isolation, the AC signal may be fed into a rectifier circuit where the AC source is converted to the DC required by many of today's electrical gadgets,
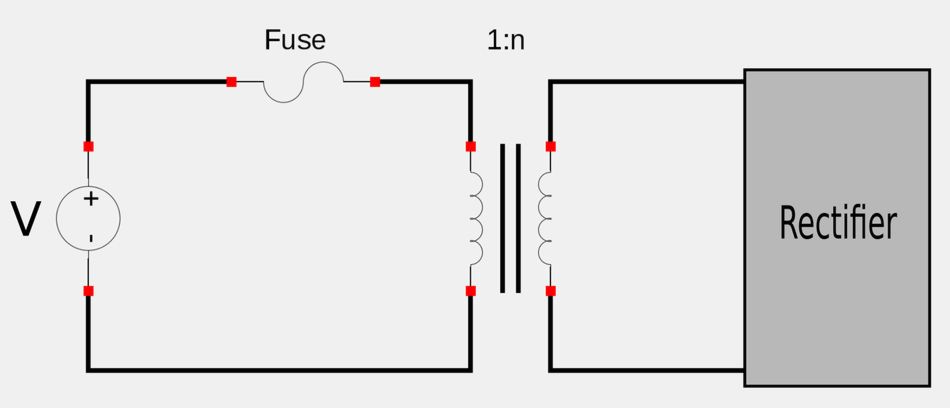
2) Coupling of Amplifier Stages.
Transformers can also be used to couple amplifier stages. Transistor amplifiers are often DC biased and since magnetic coupling does not occur with constant DC, a transformer may be used to prevent the DC voltage in one stage from affecting the DC bias of another. As a result, only the AC signal is coupled from one stage to the next.
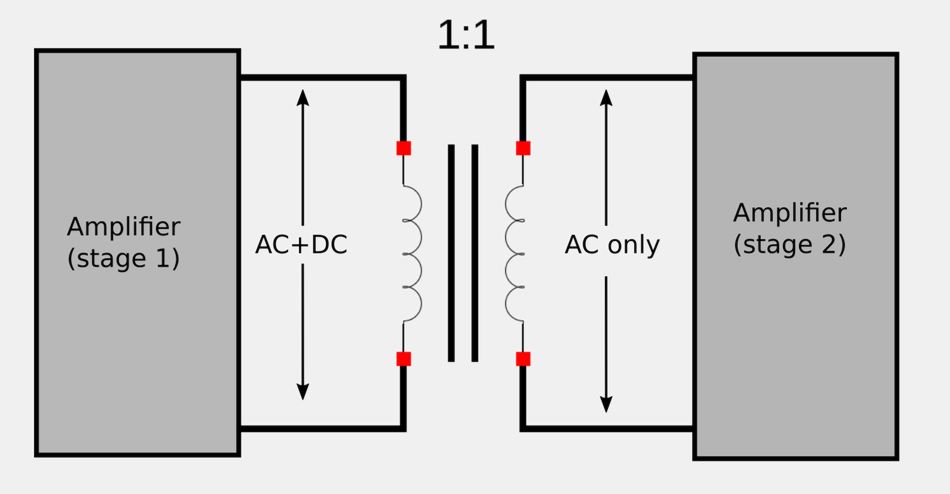
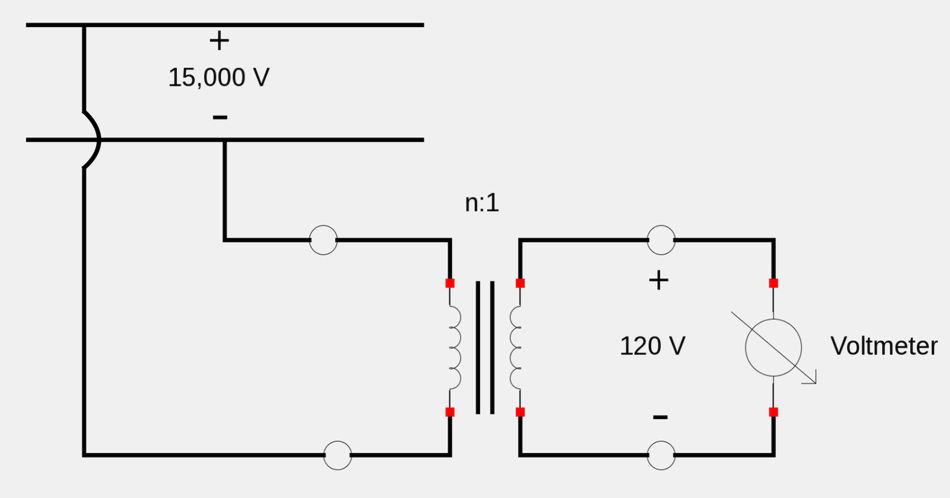
3) Measurements Across High-Voltage lines.
Applying a voltmeter across high voltage lines is unsafe. However, a voltmeter can be used to measure the stepped down voltage on the secondary side of the transformer. If the turns ratio of the transformer is known, we can then figure out the line voltage on the primary side (without having to directly measure it).
4) Impedance Matching.
We know that for maximum power transfer, the load resistance needs to match the source resistance. In cases where the resistances don't match and are of fixed values, a transformer can be used to match the load to the source (impedance matching). Consider an audio amplifier (with source resistance R_S) connected to a speaker (with load resistance R_L):
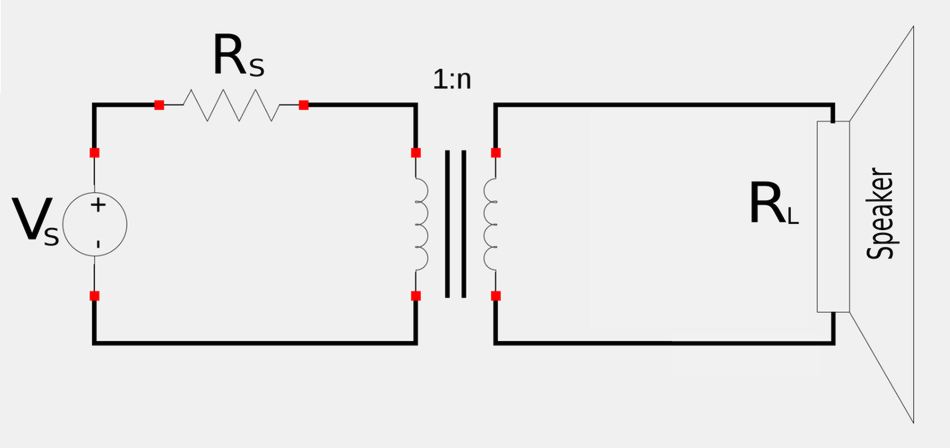
From our prior discussion on ideal transformers, we know that the reflected impedance from the load is: $$ \mathbb{Z}_R = \frac{\mathbb{Z}_L}{n^2} \qquad,(Eqn\;1)$$ Or, if the impedances are purely resistive (as is the case above): $$ R_S = \frac{R_L}{n^2} \qquad,(Eqn\;2)$$ $$ \qquad...where \; "n" \; = \; turns \; ratio \; of \; transformer $$ Therefore, equations 1 and two can be satisfied by selecting a transformer with the appropriate turns ratio (thus achieving maximum power transfer).
In the next page we will look at an example problem involving the use of a transformer for impedance matching.
Continue on to transformer application problem (impedance matching)...
