A stereo amplifier with an output impedance of 7.2 kOhm needs to be matched to a speaker with an input impedance of 8 ohm.
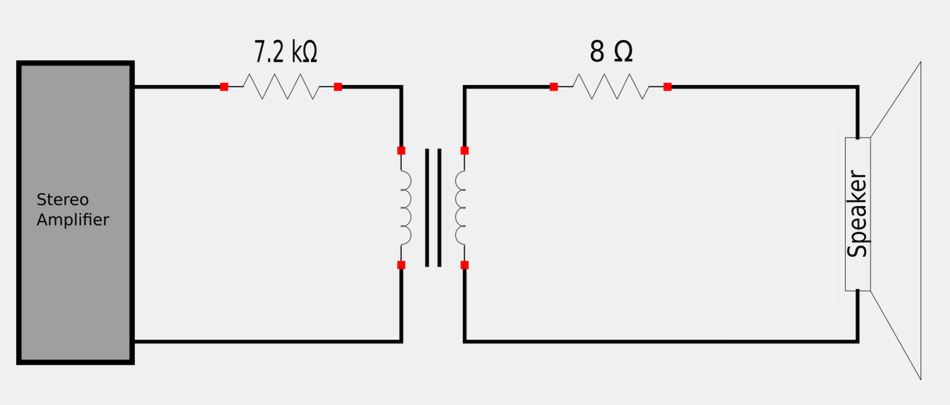
- Assuming the primary side of the transformer has 3,000 turns, determine the required number of turns in the secondary in order to achieve maximum power transfer between the amplifier and the speaker.
From the previous page, we know that for maximum power transfer between source and load, and realizing that the impedance values in our circuit are purely resistive, we need to satisfy the following equation: $$ R_S = \frac{R_L}{n^2} \qquad,(Eqn\;1)$$ ...where: $$ \qquad R_S = source \; resistance$$ $$ \qquad R_L = load \; resistance$$ $$ \qquad n = turns \; ratio$$ Rearranging equation #1 to solve for the turns ratio gives us: $$ n = \sqrt{\frac{R_L}{R_S}} $$ Plugging in the resistance values for our circuit gives us:
$$ n = \sqrt{\frac{8}{7200}} = \frac{1}{30} $$
We also know that turns ratio can be expressed as the following: $$ n = \frac{N_2}{N_1} $$ ...where N1 and N2 are the number of turns in the primary and secondary coils of the transformer respectively. Solving for the number of turns in the secondary gives us: $$ N_2 = nN_1 $$ We now plug in our calculated value for "n" and the given value for "N1": $$ N_2 = \frac{1}{30}(3000) $$
$$ N_2 = 100 \; turns $$
