Just as with general three-phase circuits, there are four possible configurations for a 3-phase transformer setup:
- wye-wye
- delta-delta
- wye-delta
- delta-wye
Power in three-phase transformers:
With all of the four configurations above, the following power expressions can be used:
Total apparent power:
$$ S_T = \sqrt{3} V_L \; I_L $$
Total real power:
$$ P_T = S_T \; \cos(\theta) $$ $$ \;\;\;\; = \sqrt{3} V_L \; I_L \; \cos(\theta) $$
Total reactive power:
$$ Q_T = S_T \; \sin(\theta) $$ $$ \;\;\;\; = \sqrt{3} V_L \; I_L \; \sin(\theta) $$
Wye-Wye connections
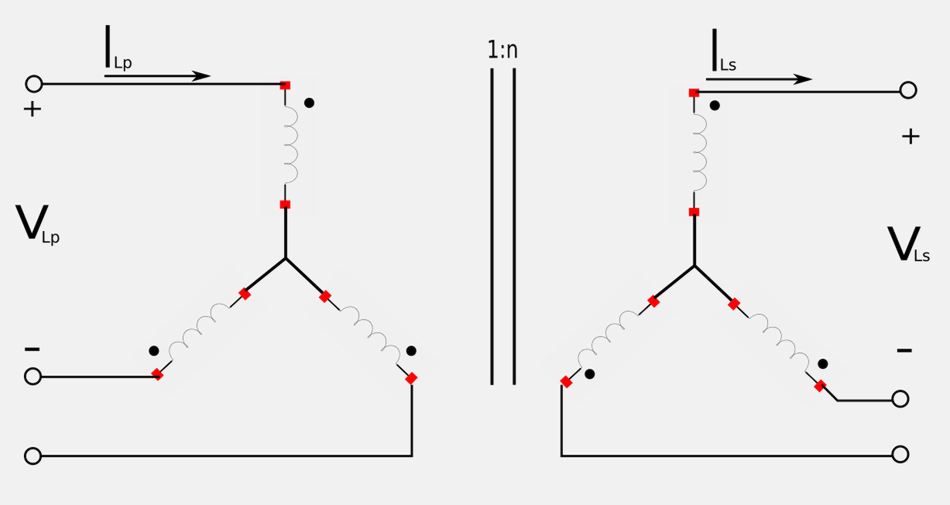
Recall the turns ratio for an ideal transformer: $$ \frac{V_2}{V_1} = \frac{N_2}{N_1} = n $$ For the Y-Y circuit above, we have: $$ \frac{V_{Ls}}{V_{Lp}} = n $$
$$ V_{Ls} = n V_{Lp} $$
Additionally, we know that the turns ratio for input and output current is: $$ \frac{I_2}{I_1} = \frac{N_1}{N_2} = \frac{1}{n} $$ So, for the Y-Y circuit we have: $$ \frac{I_{Ls}}{I_{Lp}} = \frac{1}{n} $$
$$ I_{Ls} = \frac{I_{Lp}}{n} $$
Delta-Delta connections
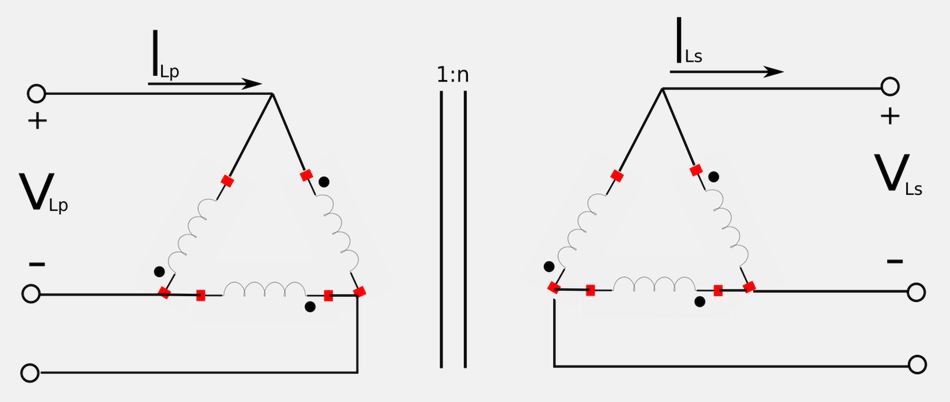
In a similar manner we have the following expressions for a delta-delta transformer configuration:
$$ V_{Ls} = nV_{Lp} $$ $$ I_{Ls} = \frac{I_{Lp}}{n} $$
Wye-Delta connections
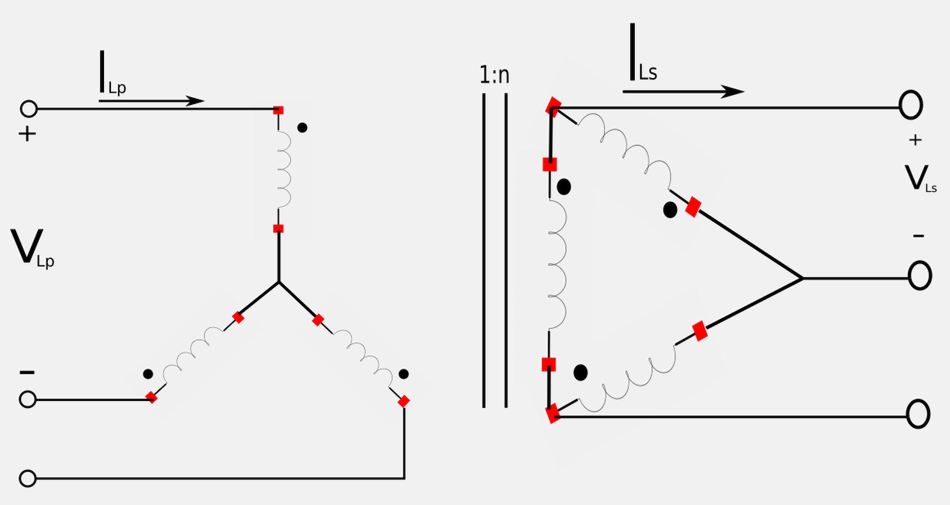
For the wye-delta transformer we have:
$$ V_{Ls} = \frac{nV_{Lp}}{\sqrt{3}} $$ $$ I_{Ls} = \frac{\sqrt{3}\;I_{Lp}}{n} $$
Delta-Wye connections
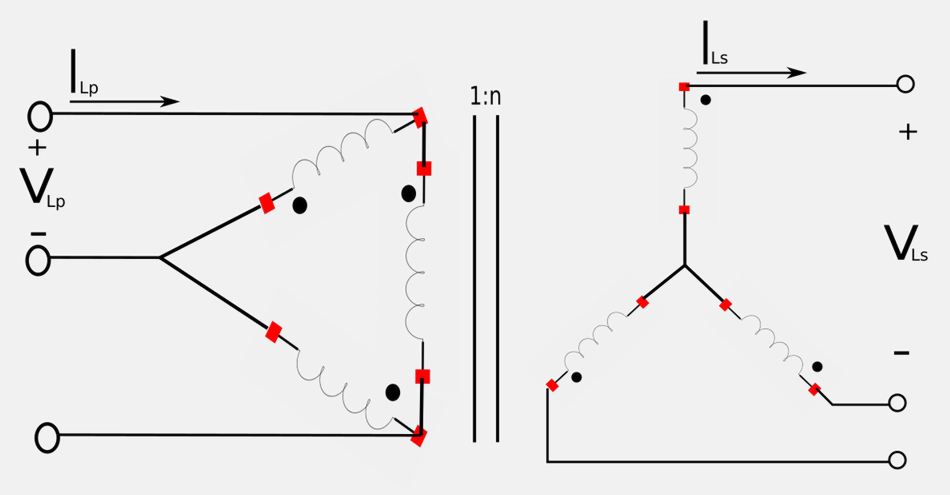
Lastly, for a delta-wye transformer configuration we have:
$$ V_{Ls} = n\sqrt{3} V_{Lp} $$ $$ I_{Ls} = \frac{I_{Lp}}{n\sqrt{3}} $$
Next we will look at an example problem involving a three-phase transformers.
Continue on to three-phase transformer example problem...
