The expression for the energy stored in an inductor is: $$ w = \frac{1}{2} Li^2 $$ With this in mind, let's consider the following circuit as we attempt to arrive at an expression for the total energy stored in a magnetically coupled circuit:
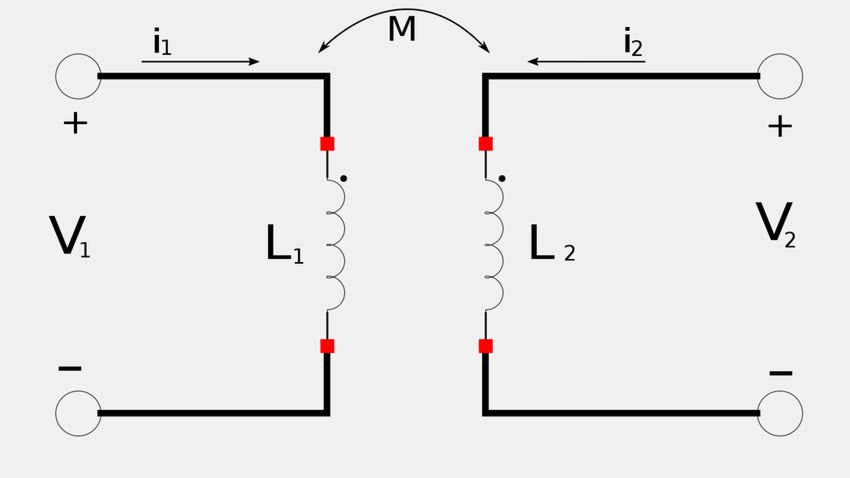
Energy stored in coil #1
In order to determine an expression for the energy stored in coil #1 (for the circuit above), we will let i1 increase from zero to its maximum value of I1 while i2 is held at zero. $$ let \; i_1 \; increase \; from \; 0 \rightarrow I_1 \; while \;i_2 = 0 $$ The power in coil #1 can be expressed in the time-domain as: $$ p_1(t) = V_1 i_1 $$ $$ p_1(t) = i_1 L_1\frac{di_1}{dt} $$ The energy stored in the circuit due to coil #1 can now be expressed as: $$ w_1 = \int_{}^{} p_1 \; dt $$ $$ \;\;\;\; = L_1 \int_{0}^{I_1} i_1 \; di_1 $$ $$ \;\;\;\; = \frac{L_1}{2} \left[ i_1^2 \right]_0^{I_1} $$
$$ w_1 = \frac{1}{2} L_1 I_1^2 \qquad (Eqn \; 1) $$
Energy stored in coil #2
In order to derive an expression for the energy stored in coil #2, we will let i1 equal its maximum value (I1) while i2 increses from zero to its maximum value of I2 $$ let \; i_2 \; increase \; from \; 0 \rightarrow I_2 \; while \; i_1 = I_1 $$ From the intro page on Mutual Inductance we know that the mutually induced voltage in coil #1 can be expressed as: $$ M_{12} \frac{di_2}{dt} $$ and the mutually induced voltage in coil #2 can be expressed as: $$ M_{21} \frac{di_1}{dt} $$ When thinking about the total power in the circuit due to the above described conditions, we have:
Ptot = (power in coil #1 due to voltage across coil) + (power in coil #1 due to mutually induced voltage) + (power in coil #2)
Expressing this mathematically gives us: $$ p_2(t) = V_1i_1 + i_1 M_{12}\frac{di_2}{dt} + V_2i_2 $$ $$ \qquad = i_1 L_1 \frac{di_1}{dt} + I_1M_{12}\frac{di_2}{dt} + i_2 L_2\frac{di_2}{dt} $$ Since the current through coil #1 is constant, the 1st term in the above expression is zero, giving us: $$ p2(t) = I_1M_{12}\frac{di_2}{dt} + i_2 L_2\frac{di_2}{dt} $$ The energy stored in the circuit can now be expressed as: $$ w_2 = \int_{}^{} p_2 \; dt $$ $$ \;\;\;\; = \int_{0}^{I_2} I_1M_{12} \; di_2 + \int_{0}^{I_2} i_2 L_2 \; di_2 $$ $$ \;\;\;\; = I_1M_{12} \; \left[ i_2 \right]_0^{I_2} \; + \frac{L_2}{2} \; \left[ i_2^2 \right]_0^{I_2} $$
$$ w_2 = M_{12} I_1 I_2 + \frac{1}{2} L_2 I_2^2 \qquad, (Eqn \; 2) $$
Total energy in coils when i_1 and i_2 have reached constant values:
$$ w = w_1 + w_2 $$ Substituting equations 1 and 2 into the above expression gives us: $$ w = \frac{1}{2} L_1 I_1^2 + M_{12} I_1 I_2 + \frac{1}{2} L_2 I_2^2 \qquad (Eqn \; 3) $$ However, let's assume that the currents reached their final values in the reverse order of what was shown above. In such a case, our procedure would have involved the following assumptions: $$ 1st: \; i_2 \; increases \; from \; 0 \rightarrow I_2 $$ $$ 2nd: \; i_1 \; increases \; from \; 0 \rightarrow I_1 $$ In this situation, if we were to repeat the entire process above, we would arrive at the following expression for the total energy in the coils once i1 and i2 reached their final values: $$ w = \frac{1}{2} L_1 I_1^2 + M_{21} I_1 I_2 + \frac{1}{2} L_2 I_2^2 \qquad (Eqn \; 4) $$ Regardless of the order in which the currents reach their final conditions, the total energy stored will be the same. This means that equations 3 and 4 must be equal. In order for them to be equal the following condition must be true: $$ M_{12} = M_{21} = M $$ Our expression for total energy now becomes: $$ w = \frac{1}{2} L_1 I_1^2 + \frac{1}{2} L_2 I_2^2 + M I_1 I_2 \qquad (Eqn \; 5)$$
Sign considerations:
You may have noticed that the process for deriving equation #5 involved the assumption that the coil currents ENTER the dotted terminals (as depicted in the circuit schematic). If this were not the case, then according to the Dot Convention the following situation would arise:
- IF one current enters one dotted terminal AND leaves the other dotted terminal
- THEN equation #5 becomes: $$ \qquad w = \frac{1}{2} L_1 I_1^2 + \frac{1}{2} L_2 I_2^2 - M I_1 I_2 \qquad,(Eqn \; 6)$$
Instantaneous energy stored in a magnetically coupled circuit:
$$ w = \frac{1}{2} L_1i_1^2 + \frac{1}{2} L_2i_2^2 \pm Mi_1i_2 $$
...where:
M = "+" if both currents enter or leave the dotted terminals.
M = "-" if otherwise.
Maximum value of mutual inductance and the coefficient of coupling:
While we won't prove it here, know that the mutual induction can't exceed the geometric mean of the self induction of the coils such that: $$ M \leq \sqrt{L_1L_2} $$
Coefficient of coupling:
The coefficient of coupling "k" determines the extent to which the mutual inductance "M" approaches its theoretical upper limit. $$ M = k\sqrt{L_1L_2} $$ "k" has the following range of values: $$ 0 \leq k \leq 1 $$ ...which means that "M" has the following range of values: $$ 0 \leq M \leq \sqrt{L_1L_2} $$ The coefficient of coupling "k" is the percentage of the total flux generated that passes through the 2nd coil. If 100% of the flux produced by one coil passes through the 2nd coil then the circuit is said to be "perfectly coupled." $$ If \; k=1 \; then \; "perfectly \; coupled" $$ $$ If \; k \gt 0.5 \; then \; "tightly \; coupled" $$ $$ If \; k \lt 0.5 \; then \; "loosely \; coupled" $$
Next we will analyze the energy stored in a magnetically coupled circuit.
Continue on to Magnetically coupled circuits and energy (example problem)...
