Given the following circuit:
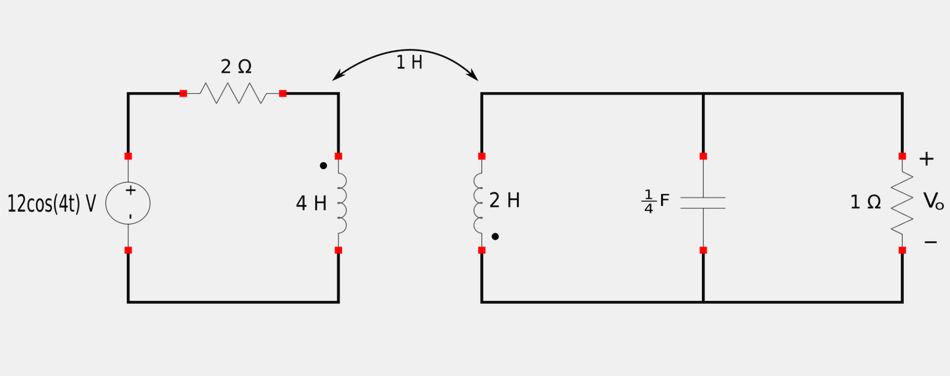
- A) Determine the coupling coefficient (k)
- B) Calculate Vo
- C) Determine the energy stored in the coupled coils at t=2s
A) Determine the coupling coefficient:
In the previous page, we learned that mutual inductance can be expressed as: $$ M = k\sqrt{L_1 L_2} $$ ...where "k" is the coefficent of coupling. The circuit schematic gives us a value of 1H for "M" as well as the labeled inductances for the two coils. Therefore: $$ k = \frac{M}{\sqrt{L_1L_2}} = \frac{1}{\sqrt{4(2)}} $$
$$ k = 0.3536 \qquad, loosely \; coupled $$
B) Calculate Vo:
We start by transforming the circuit to the frequency domain. Our plan of attack will involve mesh analysis, but first we need to determine the polarity of the induced voltages in each coil. Consider the redrawn circuit (in the frequency domain) below:
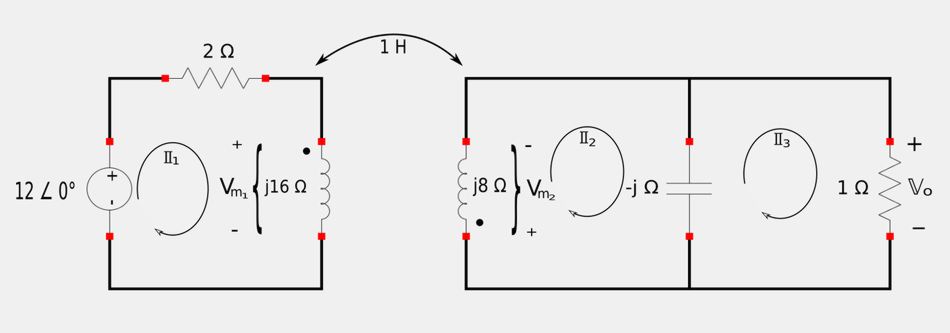
Observing the flow of our mesh currents and recalling the explanation of the Dot Convention, we see that in loop 1 the mesh current enters the dotted terminal of coil #1, which means that the polarity at the dotted terminal of the second coil is positive. Additionally, we see that the mesh current in loop 2 also enters the dotted terminal of coil #2. Therefore, the polarity at the dotted terminal of coil #1 is positive. Now understand that the mesh currents are symbolic and the direction is arbitrarily chosen, but as long as we are consistent with our signs it won't matter as far as the final answers go. The polarities are annotated in the redrawn circuit above and Vm1/Vm2 represent the induced voltages of coils #1 and #2 respectively.
Apply Kirchhoff's Voltage Law (KVL) around loop 1:
Don't forget to account for the voltage across the inductor due to i1 AND the induced voltage due to i2: $$ -12 + 2\mathbb{I}_1 + \mathbb{V}_{L_1} + \mathbb{V}_{m_1} = 0 $$
Recall from the introduction to mutual inductance page that the induced voltage in coil #1 can be expressed as: $$ \mathbb{V}_{m_1} = j \omega M \mathbb{I}_2 $$ Therefore, we now have the following expression:
$$ 2\mathbb{I}_1 + j16\mathbb{I}1 + j\omega M \mathbb{I}_2 = 12 $$ In our circuit, omega=4 and "M" is given as 1H. Therefore: $$ 2\mathbb{I}_1 + j16\mathbb{I}1 + j(4)(1) \mathbb{I}_2 = 12 $$ $$ \mathbb{I}_1(2+j16) + j4\mathbb{I}_2 = 12 $$ $$ 16.12\mathbb{I}_1 \angle 82.87^{\circ} + 4\mathbb{I}_2 \angle 90^{\circ} = 12 \qquad,(Eqn \; 1) $$
Apply Kirchhoff's Voltage Law (KVL) around loop 2:
$$ \mathbb{V}_{L_2} + \mathbb{V}_{m_2} - j(\mathbb{I}_2 - \mathbb{I}_3) = 0 $$
Once again, recall from the introduction to mutual inductance page that the induced voltage in coil #2 can be expressed as: $$ \mathbb{V}_{m_2} = j \omega M \mathbb{I}_1 $$ Therefore, we now have the following expression:
$$ \mathbb{V}_{L_2} + j \omega M \mathbb{I}_1 - j\mathbb{I}_2 + j\mathbb{I}_3 = 0 $$ Again, we know that in our circuit, omega=4 and "M" is given as 1H. Therefore: $$ j8\mathbb{I}_2 + j (4)(1) \mathbb{I}_1 - j\mathbb{I}_2 + j\mathbb{I}_3 = 0 $$ $$ j4\mathbb{I}_1 + j7\mathbb{I}_2 + j\mathbb{I}_3 = 0 $$ $$ 4\mathbb{I}_1 \angle 90^{\circ} + 7\mathbb{I}_2 \angle 90^{\circ} + \mathbb{I}_3 \angle 90^{\circ} = 0 \qquad,(Eqn \; 2) $$
Apply Kirchhoff's Voltage Law (KVL) around loop 3:
$$ -j(\mathbb{I}_3 - \mathbb{I}_2) + \mathbb{I}_3 = 0 $$ $$ -j\mathbb{I}_3 + j\mathbb{I}_2 + \mathbb{I}_3 = 0 $$ $$ j\mathbb{I}_2 + \mathbb{I}_3(1-j) = 0 $$ $$ \mathbb{I}_2 \angle 90^{\circ} + 1.414 \mathbb{I}_3 \angle 315^{\circ} = 0 \qquad,(Eqn \; 3) $$
Solve system of equations:
Putting equations 1,2 and 3 into matrix form gives us: $$ \begin{pmatrix} 16.12 \angle 82.87^{\circ}&4 \angle 90^{\circ}&0&12\\ 4 \angle 90^{\circ}&7 \angle 90^{\circ}&1 \angle 90^{\circ}&0\\ 0&1 \angle 90^{\circ}&1.414 \angle 315^{\circ}&0\\ \end{pmatrix} $$ I won't solve the matrix here. Doing so should be somewhat routine by now. Once doing so, the values of the mesh currents should be: $$ \mathbb{I}_1 = 0.8549 \angle 278.8^{\circ} $$ $$ \mathbb{I}_2 = 0.455 \angle 102.6^{\circ} $$ $$ \mathbb{I}_3 = 0.3218 \angle 57.59^{\circ} $$
Calculate Vo:
$$ \mathbb{V}_o = \mathbb{I}_3(1) = 0.3218 \angle 57.59^{\circ} = 0.3218e^{j57.59^{\circ}} \; V $$ The original question asks for Vo in the time-domain. Therefore we will multiply the above expression by e^(jwt) and take the real part of the result: $$ V_o = R_e \{ 0.3218e^{j57.59^{\circ}} \; e^{j4t} \} $$ $$ \;\;\; = R_e \{ 0.3218e^{j(4t+57.59^{\circ})} \} $$
Recall Euhler's Identity" $$ e^{j\theta} = \cos\theta + j\sin\theta $$ ...and apply it to the above expression in order to get the following:
$$ V_o = R_e \{ 0.3218\cos(4t+57.59^{\circ}) + j0.3218\sin(4t+57.59^{\circ}) \} $$
Final answer for Vo: $$ V_o = 0.3218\cos(4t+57.59^{\circ}) \; V $$
C) Determine the energy stored in the coupled coils at t=2s:
Recall from the previous page that we can define the instantaneous energy in the coils of our circuit as: $$ w = \frac{1}{2} L_1i_1^2 + \frac{1}{2} L_2i_2^2 + Mi_1i_2 \qquad(Eqn\;4)$$ In our case "M" is positive because the drawn mesh currents enter both of the dotted terminals. Specifically, we want the value of the instantaneous energy at t=2s. Therefore we need to calculate the values of mesh currents 1 and 2 at t=2s. When transformed to the time domain, the mesh currents are: $$ i_1 = 0.8549 \cos(4t+278.8^{\circ}) $$ $$ i_2 = 0.455\cos(4t+102.6^{\circ}) $$ However, don't forget tha the two expressions above include the given angular frequency of 4 radians, but our phase angle is in degrees. If we were to evaluate the expressions as they now appear by plugging in "2" for "t" and then add the phase angles, we would get an incorrect result. Therefore we need to first convert the phase angles from degrees to radians. $$ 278.8^{\circ} = 278.8^{\circ} \Big( \frac{\pi}{180^{\circ}} \Big) = 4.866 \; rad $$ $$ 102.6^{\circ} = 102.6^{\circ} \Big( \frac{\pi}{180^{\circ}} \Big) = 1.791 \; rad $$ Our expressions now become: $$ i_1 = 0.8549 \cos(4t+4.866) $$ $$ i_2 = 0.455\cos(4t+1.791) $$ Plugging in "2" for "t" in the above two expressions gives us the following values: $$ i_1 = 0.8168 \; A $$ $$ i_2 = -0.4248\;A $$ Notice that we get a negative value for i2 which means that the assumed direction of the mesh current in loop 2 was wrong and therefore the the polarity of the induced voltage in coil #1 is incorrect as well. That's ok however because we were not given specific current flow directions for loop 2 and or final answer will still be correct as long as we are consistent with the signs. We now substitute these current values (as well as the inductance values for the coils) into equation #4: $$ w = \frac{1}{2} L_1i_1^2 + \frac{1}{2} L_2i_2^2 + Mi_1i_2 $$ $$ w(2) = \frac{1}{2} 4(0.8168)^2 + \frac{1}{2} 2 (-0.4248)^2 + (1) (0.8168) (-0.4248) $$
The energy stored in the coupled coils at t=2s is: $$ w(2) = 1.168 \; J $$
