For the following circuit:
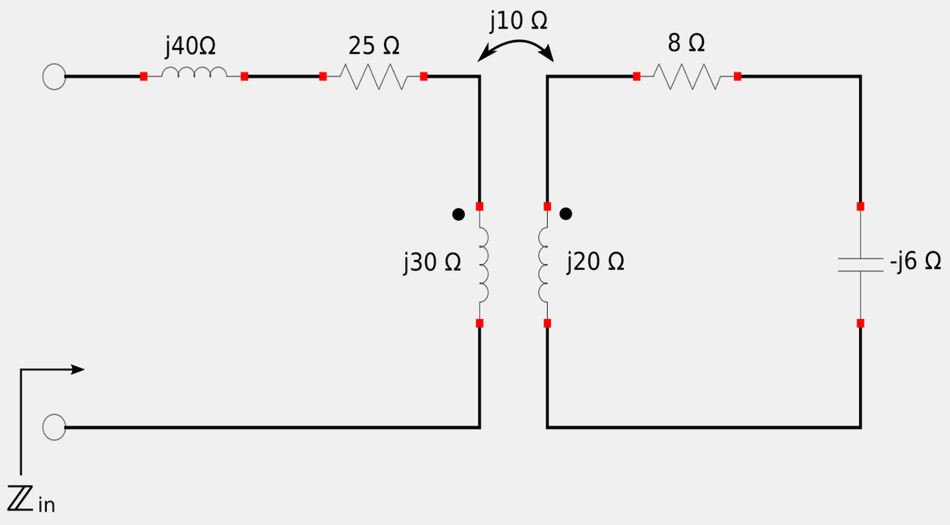
- A) Determine Zin using the concept of reflected impedance.
- B) Determine Zin using a Τ-equivalent circuit.
A) Determine Zin using the concept of reflected impedance.
Compare the circuit above with the circuit we used on the previous page that was used to derive the expression for input impedance:
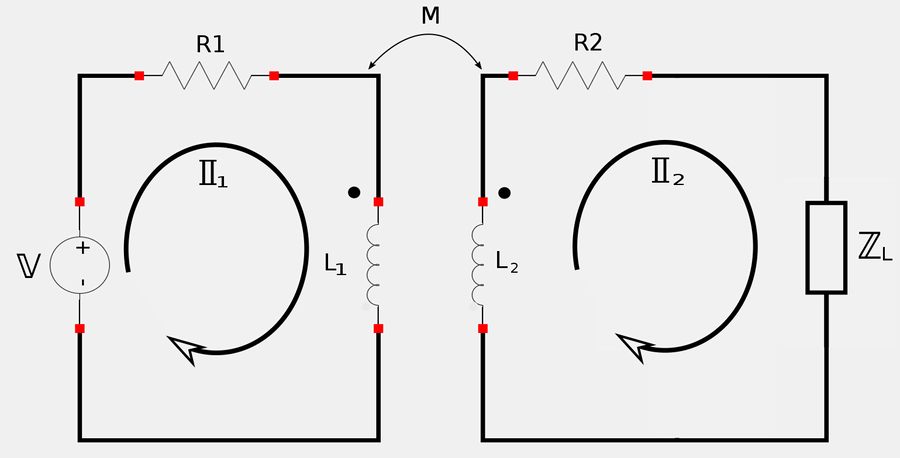
If we equate elements of both elements we get: $$ R_1 = 25+j40 \; \Omega$$ $$ R_2 = 8 \; \Omega$$ $$ \omega L_1 = 30 $$ $$ \omega L_2 = 20 $$ $$ \omega M = 10 $$ $$ \mathbb{Z}_L = -j6 \; \Omega $$
Recall the expression for input impedance of a transformer: $$ \mathbb{Z}_{in} = primary\;impedance\;+reflected\;impedance $$ $$ \;\;\;\;\; = R_1+j\omega L_1 + \frac{\omega^2 M^2}{R_2 + j\omega L_2 + \mathbb{Z}_L} $$ Substituting the terms for our circuit into this expression for input impedance gives us: $$ \mathbb{Z}_{in} = 25 + j40 + j30 + \frac{10^2}{8+j20-j6} $$ $$ \;\;\;\;\; = 25+j70 + \frac{100}{8+j14} $$
$$ \mathbb{Z}_{in} = 28.1 + j64.6 \; \Omega $$
B) Determine Zin using a Τ-equivalent circuit.
Start by recognizing that our Τ-equivalent circuit will take the following form:
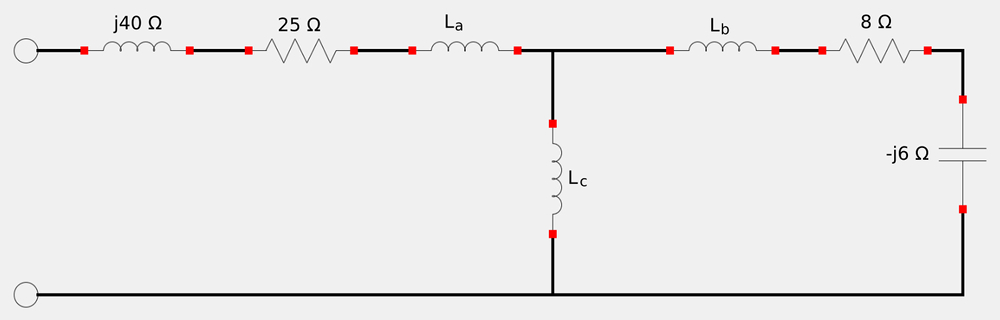
... and will be the equivalent of our original magnetically coupled circuit shown below:

Also, recall the expressions for transforming a magnetically-coupled circuit to a Τ-equivalent circuit: $$ L_a = L_1 - M $$ $$ L_b = L_2 - M $$ $$ L_c = M $$
Determine an expression for inductor "a":
For inductor "a" we have: $$ L_a = L_1 - M $$ Our goal however, is to get impedance values since our eventual goal is to determine Zin. Therefore, we convert the above inductance values to impedances: $$ j\omega L_a = j\omega L_1 - j\omega M $$
Remember that above we determined the following: $$ \omega L_1 = 30 $$ $$ \omega L_2 = 20 $$ $$ \omega M = 10 $$ ...therefore:
$$ j\omega L_a = j30-j10 $$
$$ j\omega L_a = j20 \; \Omega $$
Determine an expression for inductor "b":
For inductor "b", we have: $$ L_b = L_2 - M $$ Once again we want impedance values, so convert the above inductances to impedances: $$ j\omega L_b = j\omega L_2 - j\omega M $$ $$ \qquad = j20 - j10 $$
$$ j\omega L_b = j10 \; \Omega $$
Determine an expression for inductor "c":
For inductor "c", we have: $$ L_c = M $$ Converted to impedance gives us: $$ j\omega L_c = j\omega M $$
$$ j\omega L_c = j10 \; \Omega $$
Solve for Zin:
If we plug our derived expresions for inductors "a" "b" and "c" into the Τ-equivalent circuit we have the following:
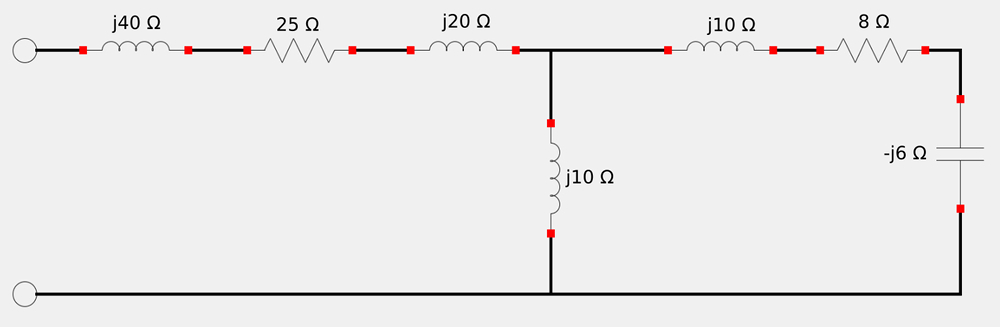
We now use the rules for impedances in series and parrallel to get Zin: $$ \mathbb{Z}_{in} = 25 + j60 + [j10 || 8+j4] $$ $$ \;\;\;\;\; = 25+j60 + \frac{1}{\frac{1}{j10} + \frac{1}{8+j4}} $$
$$ \mathbb{Z}_{in} = 70.45 \angle 66.51^{\circ} = 28.08+j64.62 \; \Omega $$
