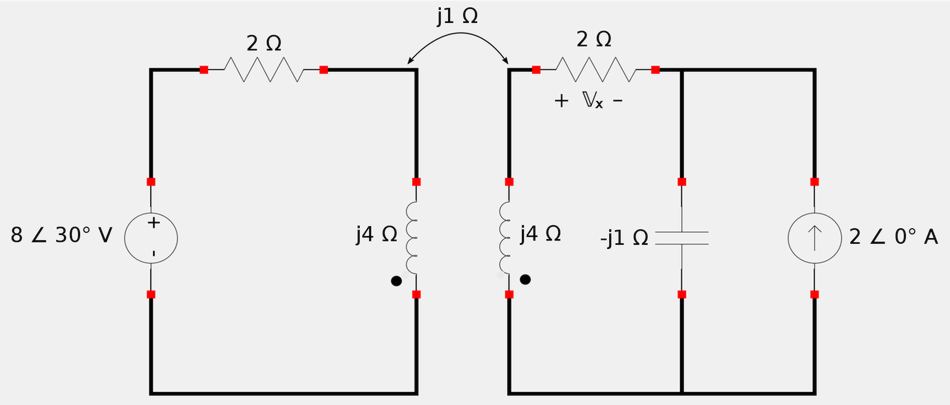
For the following circuit, determine Vx:
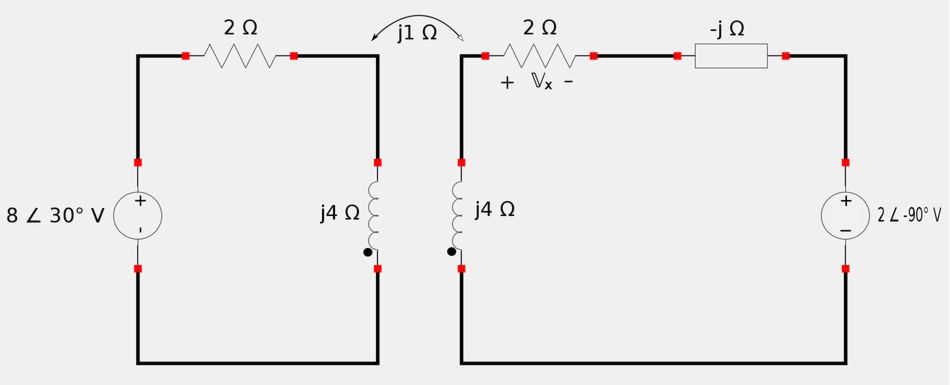
Before proceeding, we will make the circuit easier to analyze by transforming the current source in parallel with the capacitor to it's Thevenin equivalent. $$ \mathbb{V}_{th} = \mathbb{I}_N \mathbb{Z}_{th} $$ $$ \mathbb{V}_{th} = (2 \angle 0^{\circ}) (-j) $$ $$ \mathbb{V}_{th} = 2 \angle (-90^{\circ}) $$ Our transformed circuit is shown below:
Determine the polarity of the mutually induced voltages
We will use mesh analysis for both loops and use symbolic mesh-currents flowing clockwise around the loops. With this in mind, in the left-most loop, we see that the current leaves the dotted terminal of the coil. Therefore the polarity is negative at the dotted terminal in the second loop. Conversely, in the second loop, we see that the current enters the dotted terminal of the coil. Therefore the polarity is positive at the dotted terminal of loop #1.
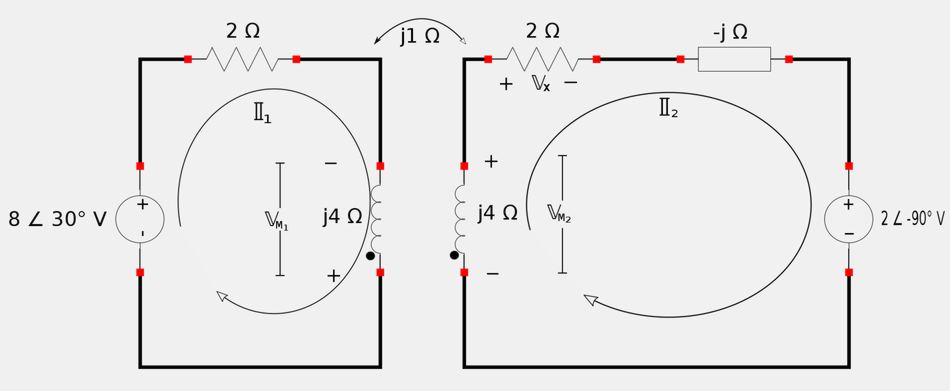
In this example you notice that we are not given a value for the mutual inductance between the two coils (no value given for "M"). In the previous page we learned that our mutually induced voltages for this circuit would be defined as: $$ V_1 = M \Big( \frac{di_2}{dt} \Big) , \;\;\; \mathbb{V}_1 = j \omega M \mathbb{I}_2 $$ $$ V_2 = M \Big( \frac{di_1}{dt} \Big) , \;\;\; \mathbb{V}_2 = j \omega M \mathbb{I}_1 $$ "jwM" can be thought of as the impedance between the two magnetically coupled coils and in our schematic it is labled as being "j1 ohms". Therefore: $$ j \omega M = j1 \; \Omega $$ Now, keeping in mind the polarity of the induced voltages that we just determined, as well at the direction of travel as we apply Kirchhoff's voltage law around the loops, we will have the following mutually induced voltages: $$ \mathbb{V}_{M1} = -j \mathbb{I}_2 $$ $$ \mathbb{V}_{M2} = -j \mathbb{I}_1 $$ Don't confuse the polarity of the induced voltages with the polarity of the non-induced voltage across the inductor (which will be positive and added separately).
Apply Kirchhoff's Voltage Law (KVL) around the loops:
Applying KVL around loop #1 gives us: $$ -8 \angle 30^{\circ} + 2\mathbb{I}_1 + \mathbb{V}_{L1} + V_{M1} = 0 $$ $$ -8 \angle 30^{\circ} + 2\mathbb{I}_1 + j4\mathbb{I}_1 -j \mathbb{I}_2 = 0 $$ $$ \mathbb{I}_1(2+j4) -j\mathbb{I}_2 = 8 \angle 30^{\circ} $$ $$ 4.472\mathbb{I}_1 \angle 63.43^{\circ} + \mathbb{I}_2 \angle (-90^{\circ}) = 8 \angle 30^{\circ} \qquad (Eqn \; 1) $$ Applying KVL around loop #2 gives us: $$ 2 \angle (-90^{\circ}) + \mathbb{V}_{L2} + V_{M2} + 2\mathbb{I}_2 - j\mathbb{I}_2 = 0 $$ $$ 2 \angle (-90^{\circ}) + j4\mathbb{I}_2 - j \mathbb{I}_1 + 2\mathbb{I}_2 - j\mathbb{I}_2 = 0 $$ $$ -j\mathbb{I}_1 + \mathbb{I}_2(2+j3) = -2 \angle (-90^{\circ}) $$ $$ \mathbb{I}_1 \angle (-90^{\circ}) + 3.606\mathbb{I}_2 \angle 56.31^{\circ} = 2 \angle 90^{\circ} \qquad(Eqn \; 2) $$
Solve system of equations
You could solve the system of equations for equations 1 and 2 by means of substitution but we will use this as an opportunity to refresh our knowledge of Cramer's Rule. Putting equations 1 and 2 into matrix form gives us: $$ \begin{pmatrix} 4.472\angle 63.43^{\circ}&1\angle (-90^{\circ})&8\angle 30^{\circ}\\ 1\angle (-90^{\circ})&3.606\angle 56.31^{\circ}&2\angle 90^{\circ}\\ \end{pmatrix} $$
$$ D = \begin{vmatrix} 4.472\angle 63.43^{\circ}&1\angle (-90^{\circ})\\ 1\angle (-90^{\circ})&3.606\angle 56.31^{\circ}\\ \end{vmatrix} $$ $$ = (4.472\angle 63.43^{\circ})(3.606\angle 56.31^{\circ}) - (1\angle (-90^{\circ}))(1\angle (-90^{\circ})) $$ $$ D = 15.66 \angle 116.5^{\circ} $$
$$ D_{\mathbb{I}_2} = \begin{vmatrix} 4.472\angle 63.43^{\circ}&8\angle 30^{\circ}\\ 1\angle (-90^{\circ})&2\angle 90^{\circ}\\ \end{vmatrix} $$ $$ = (4.472\angle 63.43^{\circ})(2\angle 90^{\circ}) - (1\angle (-90^{\circ}))(8\angle 30^{\circ}) $$ $$ D_{\mathbb{I}_2} = 16.23 \angle 137.7^{\circ} $$
$$ \mathbb{I}_2 = \frac{D_{\mathbb{I}_2}}{D} = \frac{16.23 \angle 137.7^{\circ}}{15.66 \angle 116.5^{\circ}} $$ $$ \mathbb{I}_2 = 1.036 \angle 21.2^{\circ} $$
Solve for Vx
We can now use Ohm's Law to solve for Vx: $$ \mathbb{V}_x = 2\mathbb{I}_2 $$ $$ \;\;\;\; = 2(1.036 \angle 21.2^{\circ}) $$
$$ \mathbb{V}_x = 2.072 \angle 21.2^{\circ} \; V $$
