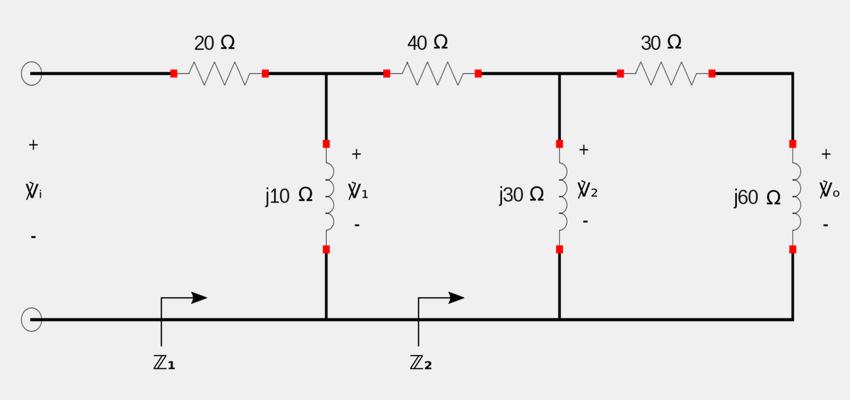
A) Calculate the phase-shift.

B) State whether the phase-shift is leading or lagging.

C) Determine the magnitude of the output when the input is 120V

We notice that this circuit consists of three stages with 3 phase-shifting circuits cascaded together.

Step 1: Determine required equivalent impedances (Z1 and Z2)

We will be using the principle of voltage division for impedances and as such we need to calculate the equivalent impendances for the first two stages.

Equivalent impedance for 2nd stage:

Starting with the equivalent impedance for the 2nd stage we have: $$ \mathbb{Z}_2 = j30 \; || \; (30+j60) $$ Using the principle of impedances in parallel, we get: $$ \frac{1}{\mathbb{Z}_2} = -j\frac{1}{30} + \frac{1}{30+j60} $$ Multiply the 2nd term by its complex conjugate: $$ \frac{1}{\mathbb{Z}_2} = -j\frac{1}{30} + \frac{1}{30+j60} \Big( \frac{30-j60}{30-j60} \Big)$$ $$ = -j\frac{1}{30} + \frac{30-j60}{4500} $$ $$ = -j\frac{1}{30} + \frac{1}{150} - j\frac{1}{75} $$ $$ \frac{1}{\mathbb{Z}_2} = \frac{1}{150} - j\frac{7}{150} $$ Taking the inverse of both sides and multiplying the right side by the complex conjugate: $$ \mathbb{Z}_2 = \frac{1}{\frac{1}{150} - j\frac{7}{150}} \Big( \frac{\frac{1}{150} + j\frac{7}{150}}{\frac{1}{150} + j\frac{7}{150}} \Big) $$ $$ = \frac{\frac{1}{150} + j\frac{7}{150}}{\frac{1}{450}} $$

$$ \mathbb{Z}_2 = (3 + j21) \Omega = 21.21 \angle 81.87^{\circ} $$

Equivalent impedance for 1st stage:

For the equivalent impedance for the 1st stage we have: $$ \mathbb{Z}_1 = j10 \; || \; (40+\mathbb{Z}_2) $$ Using the principle of impedances in parallel, we get: $$ \frac{1}{\mathbb{Z}_1} = -j\frac{1}{10} + \frac{1}{40+3+j21} $$ $$ = -j\frac{1}{10} + \frac{1}{43+j21} $$ Multiplying by complex conjugate: $$ = -j\frac{1}{10} + \frac{1}{43+j21} \Big( \frac{43-j21}{43-j21} \Big)$$ $$ \frac{1}{\mathbb{Z}_1} = -j\frac{1}{10} + \frac{43-j21}{2290} $$ $$ = -j\frac{1}{10} + \frac{43}{2290} - j\frac{21}{2290} $$ $$ \frac{1}{\mathbb{Z}_1} = 0.0188 - j0.1092 $$ Taking the inverse of both sides and multiplying by the complex conjugate: $$ \mathbb{Z}_1 = \frac{1}{0.0188 - j0.1092} \Big( \frac{0.0188 + j0.1092}{0.0188 + j0.1092} \Big) $$ $$ \mathbb{Z}_1 = \frac{0.0188 + j0.1092}{0.0123} $$

$$ \mathbb{Z}_1 = (1.528+j8.878) \Omega = 9.009 \angle 80.23^{\circ} $$

Step 2: Determine the output of the 1st stage:

We now proceed to use the concept of voltage division to determine the output of the first stage: $$ \mathbb{V}_1 = \frac{\mathbb{Z}_1}{20+\mathbb{Z}_1} \; \mathbb{V}_i $$ $$ = \frac{9.009 \angle 80.23^{\circ}}{21.528+j8.878} \; \mathbb{V}_i $$ After converting the denominator to polar form we get: $$ \mathbb{V}_1 = \frac{9.009 \angle 80.23^{\circ}}{23.29 \angle 22.41^{\circ}} \; \mathbb{V}_i $$ Using the law of division of complex numbers and noting that Vi=120 V: $$ \mathbb{V}_1 = (0.3868 \angle 57.82^{\circ}) (120) $$

$$ \mathbb{V}_1 = 46.42 \angle 57.82^{\circ} $$

Step 2: Determine the output of the 2nd stage:

We again use voltage division to determine the output of the second stage: $$ \mathbb{V}_2 = \frac{\mathbb{Z}_2}{40+\mathbb{Z}_2} \; \mathbb{V}_1 $$ $$ = \frac{21.21 \angle 81.87^{\circ}}{43+j21} \; \mathbb{V}_1 $$ Once we convert the denominator to polar form we get: $$ \mathbb{V}_2 = \frac{21.21 \angle 81.87^{\circ}}{47.85 \angle 26.03^{\circ}} \; \mathbb{V}_1 $$ Using the principle of division for complex numbers and substituting our above-determined value for V1 gives us: $$ \mathbb{V}_2 = (0.4433 \angle 55.84^{\circ}) (46.42 \angle 57.82^{\circ}) $$ Using the principle of multiplication of complex numbers in polar form: $$ \mathbb{V}_2 = (0.4433)(46.42) \angle (55.84^{\circ} + 57.82^{\circ}) $$

$$ \mathbb{V}_2 = 20.58 \angle 113.7^{\circ} $$

Step 3: Determine the output of the 3rd stage (Vo):

Voltage division is onced again used to determine the final output of the circuit: $$ \mathbb{V}_o = \frac{j60}{30+j60} \; \mathbb{V}_2 $$ $$ = \frac{60 \angle 90^{\circ}}{67.08 \angle 63.43^{\circ}} \; \mathbb{V}_2 $$ Using the principle of division for complex numbers and substituting our above-determined value for V2 gives us: $$ \mathbb{V}_o = (0.8945 \angle 26.57^{\circ}) (20.58 \angle 113.7^{\circ}) $$

Output of circuit:

$$ \mathbb{V}_o = 18.41 \angle 140.3^{\circ} $$

From our determined value for Vo, we can state that: $$ A) \; Phase \; shift: \; 140.3^{\circ} $$ $$ B) \; Output \; with \; respect \; to \; input: $$ $$ \qquad \qquad positive \; shift = leading $$ $$ C) \; Magnitude \; of \; output: $$ $$ \qquad \qquad |\mathbb{V}_o| = 18.41 V $$

Let's take a look at one more example of phase-shifting circuits.

Continue on to phase shifting circuits example problem #3.