For the following circuit with the variable resistor (potentiometer) having a value of "R":

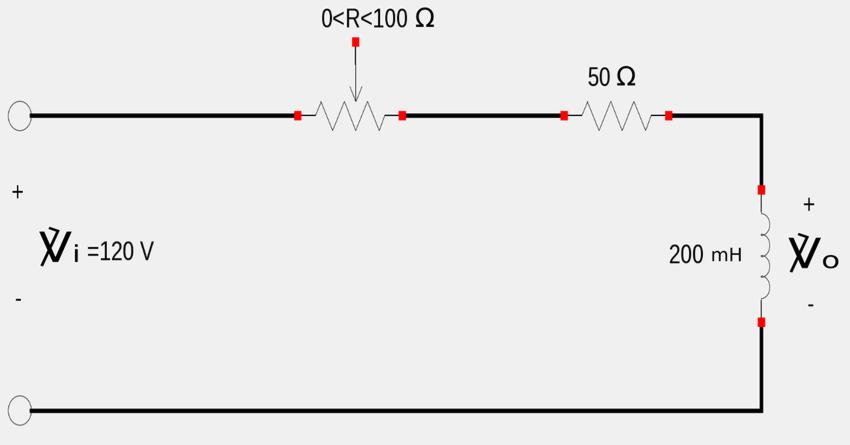
A) Determine Vo when "R" is at maximum.

B) Determine Vo when "R" is at minimum.

C) Determine the value of "R" that will produce a phase-shift of 45 degrees.

Note: Assume the following: $$frequency,(f)=60Hz$$ $$angularfrequency,(\omega )=120\pi =377\frac{rad}{s}$$ When the term "Vo" is used, it will be defined as the output voltage in phasor form.

Before proceeding, we need to determine the impedance of the inductor. Recall from the Impedance and admittance introduction page that the impedance of an inductor is defined as follows: $${\mathbb{Z}}_L=j\omega L$$ ...so for the inductor in our given circuit we have: $${\mathbb{Z}}_L=j(377)(200\times {10}^{-3})$$

$${\mathbb{Z}}_L=j75.4\mathrm{\Omega }$$

Part A: Determine Vo when "R" is maximum:

When "R" is at it's maximum value we have: $$R=100\mathrm{\Omega }$$ In order to find Vo under such a circumstance, we will use the principle of voltage division as explained in the Phase-shifting circuits introduction page. By applying voltage division to our situation we get: $${\mathbb{V}}_o=\frac{{\mathbb{Z}}_L}{{\mathbb{Z}}_L+100+50}{\mathbb{V}}_i$$ Substituting our above-determined value for Z_L $${\mathbb{V}}_o=\frac{j75.4}{150+j75.4}{\mathbb{V}}_i$$ We now convert the complex numbers in the numerator and denominator of the above expression from rectangular to polar form and get: $${\mathbb{V}}_o=\frac{75.4\mathrm{\angle }{90}^{\circ }}{167.9\mathrm{\angle }{26.69}^{\circ }}{\mathbb{V}}_i$$ Using the division property for complex numbers (found in the Compex numbers tutorial) and substituting 120 for Vi, we get: $${\mathbb{V}}_o=(0.4491\mathrm{\angle }{63.31}^{\circ })(120)$$ Multiplying the complex number by 120 gives us our final answer.

Vo when R is at maximum value:

$${\mathbb{V}}_o=53.89\mathrm{\angle }{63.31}^{\circ },whenR=100\mathrm{\Omega }$$

Part B: Determine Vo when "R" is at minimum:

When "R" is at it's minimum value we have: $$R=0\mathrm{\Omega }$$ We will again use voltage division to find the output phasor voltage of the circuit. $${\mathbb{V}}_o=\frac{{\mathbb{Z}}_L}{{\mathbb{Z}}_L+0+50}{\mathbb{V}}_i$$ Substituting our above-determined value for the impedance of the inductor: $${\mathbb{V}}_o=\frac{j75.4}{50+j75.4}{\mathbb{V}}_i$$ We again convert the complex numbers in the numerator and denominator of the above expression from rectangular to polar form and get: $${\mathbb{V}}_o=\frac{75.4\mathrm{\angle }{90}^{\circ }}{90.47\mathrm{\angle }{56.45}^{\circ }}{\mathbb{V}}_i$$ Using the division property for complex numbers (found in the Compex numbers tutorial) and substituting 120 for Vi, we get: $${\mathbb{V}}_o=(0.8334\mathrm{\angle }{33.55}^{\circ })(120)$$ Multiplying the complex number by 120 gives us our final answer.

Vo when R is at minimum value:

$${\mathbb{V}}_o=100\mathrm{\angle }{33.55}^{\circ },whenR=0\mathrm{\Omega }$$

Part C: Determine the value of "R" that will produce a phase-shift of 45 degrees:

Our goal is to achieve: $$\theta ={45}^{\circ }$$ Recall from the intro to phase shifting circuits page as well as the intro to Impedance and Admittance page that: $$\theta =ta{n}^{-1}(\frac{X}{R_{tot}})$$ For our circuit, R_tot is the sum of the 50 ohm resistor and the value of the potentiometer. Therefore we have: $$\theta =ta{n}^{-1}(\frac{X}{50+R})={45}^{\circ },(Eqn1)$$ Remember that "X" is reactance and in our case it is inductive in nature. From the Impedance and Admittance page, we know that: $${\mathbb{Z}}_L=j\omega L$$ From that same page we also know that: $$X=I_m\{\mathbb{Z}\}$$ therefore: $$X_L=I_m\{{\mathbb{Z}}_L\}=I_m\{j\omega L\}$$ $$X_L=\omega L$$ Equation #1 now becomes: $${45}^{\circ }=ta{n}^{-1}(\frac{X_L}{50+R})$$ $${45}^{\circ }=ta{n}^{-1}(\frac{\omega L}{50+R})$$ Substitute the given values for omega and the inductor: $${45}^{\circ }=ta{n}^{-1}(\frac{377(200\times {10}^{-3})}{50+R})$$ Take the tangent of both sides of the equation: $$\tan (45)=\frac{377(200\times {10}^{-3})}{50+R}$$ $$1=\frac{75.4}{50+R}$$ $$50+R=75.4$$ Solving for R gives us our final answer:

Value for "R" that gives a 45 degree phase-shift

$$R=25.4\mathrm{\Omega }$$