Design a circuit to provide a phase shift of 90 degrees (leading) and determine the output voltage (relative to input)

Since the phase shift is greater than 60 degrees, we will chain together two phase shifting circuits of 45 degrees each. Recall from the previous page that: $$ \theta = tan^{-1} \Big( \frac{X_c}{R} \Big) $$ and if $$ \frac{X_c}{R} = 1 $$ then: $$ \theta = 45^{\circ} $$ For our circuit, we will let: $$ R = |X_c| = 20\Omega $$ Our circuit will look like the following. Remember that when impedances are capacitive in nature, they are associated with a "-j" :

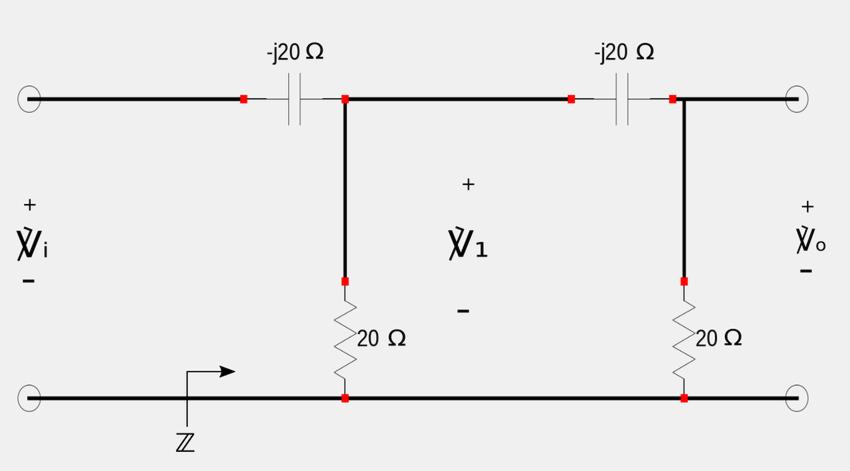
Step 1: determine the output voltage of the 1st stage:

The equivalent impedance labeled Z with the arrow is determined using the laws of series and parallel impedances: $$ \mathbb{Z} = 20\Omega \; || \; [20-j20] \Omega $$ $$ = \frac{1}{\frac{1}{20} + \frac{1}{20-j20}} $$ We now multiply the second term in the denominator by its complex conjugate: $$ = \frac{1}{\frac{1}{20} + \frac{1}{20-j20} \Big( \frac{20+j20}{20+j20} \Big)} $$ $$ = \frac{1}{\frac{1}{20} + \frac{20+j20}{800}} $$ $$ = \frac{1}{\frac{1}{20} + \frac{1}{40} + \frac{j}{40}} $$ $$ = \frac{1}{\frac{3}{40} + \frac{j}{40}} $$ $$ = \frac{1}{\frac{3+j}{40}} $$ $$ = \frac{40}{3+j} $$ We again multiply the above expression by its complex conjugate: $$ = \frac{40}{3+j} \Big( \frac{3-j}{3-j} \Big) $$ $$ = \frac{120-j40}{10} $$ After evaluating the above expression we get the following equivalent impedance:

$$ \mathbb{Z} = (12-j4) \Omega $$

We can now determine the output of the 1st stage using simple voltage division. (As explained in the intro to phase-shifting circuits page.)

$$ \mathbb{V}_1 = \frac{\mathbb{Z}}{\mathbb{Z}-j20} \;\mathbb{V}_i $$ $$ = \frac{12-j4}{12-j4-j20} \;\mathbb{V}_i $$ $$ = \frac{12-j4}{12-j24} \;\mathbb{V}_i $$ We now convert the complex numbers in the numerator and denominator of the above expression from rectangular to polar form. (Refer to the Compex numbers tutorial if you need a refresher on this.) $$ \mathbb{V}_1 = \frac{12.65 \angle (-18.43^{\circ})}{26.83 \angle (-63.43^{\circ})} \;\mathbb{V}_i $$ $$ = \frac{12.65}{26.83} \angle(-18.43 - (-62.43)) \;\mathbb{V}_i $$ After evaluating the above expression, we obtain the output voltage for the 1st stage:

$$ \mathbb{V}_1 = 0.4715 \angle 45^{\circ} \;\mathbb{V}_i \qquad(Eqn \; 1)$$

Step 2: Determine the output voltage of 2nd stage (Vo):

Once again we use voltage division to determine the output voltage of the 2nd stage: $$ \mathbb{V}_o = \frac{20}{20-j20} \; \mathbb{V}_1 $$ Substituting equation #1 for V1 gives us the following: $$ \mathbb{V}_o = \Big( \frac{20}{20-j20} \Big) (0.4715 \angle 45^{\circ}) \;\mathbb{V}_i $$ We now multiply the 1st term in the above expression by its complex conjugate: $$ = \Big( \frac{20}{20-j20} \Big) \Big( \frac{20+j20}{20+j20} \Big) (0.4715 \angle 45^{\circ}) \;\mathbb{V}_i $$ $$ = \Big( \frac{400+j400}{800} \Big) (0.4715 \angle 45^{\circ}) \;\mathbb{V}_i $$ $$ \mathbb{V}_o = \Big( \frac{1}{2} + j\frac{1}{2} \Big) (0.4715 \angle 45^{\circ}) \;\mathbb{V}_i $$ We now convert the complex number in the 1st term from rectangular to polar form: $$ = (0.7071 \angle 45^{\circ}) (0.4715 \angle 45^{\circ}) \;\mathbb{V}_i $$ ...and proceed to evaluate using the laws of operations for complex numbers (found in the Compex numbers tutorial) $$ = \Big( (0.7071)(0.4715) \angle(45^{\circ} + 45^{\circ}) \Big) \;\mathbb{V}_i $$ Once the above expression is evaluated, we finally obtain our output voltage relative to the input:

$$ \mathbb{V}_o = 0.333 \mathbb{V}_i \angle 90^{\circ} $$ Take note of the fact that while the output has a leading phase angle of 90 degrees, it is only about 1/3 of the input voltage.

(Side note)

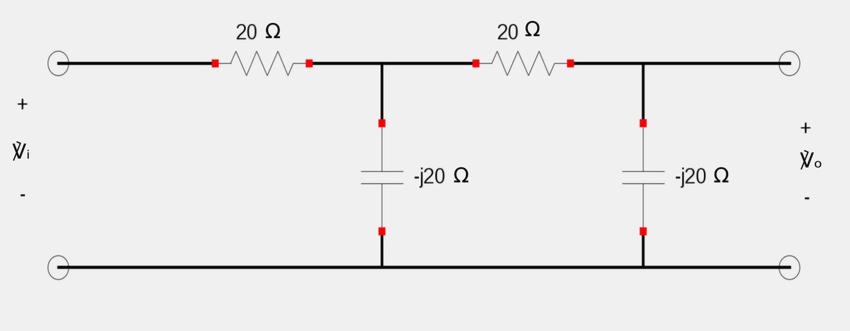
On the other hand, if we wanted to obtain a 90 degree lagging phase, the circuit would look like the following:

Let's take another look at an example problem involving phase-shifting circuits.

Continue on to phase shifting circuits example problem #2.